�������ȗ��R�ɂ�鏑�����݂̍폜�ɂ��āF �����p�V �Ƃ݂������:������Ȃ����͂����ɏ����Ă�454 YouTube����>2�{ ->�摜>37��
����A�摜���o �b�b
���̌f����
�ގ��X��
�f���ꗗ �l�C�X�� ����l�C��
���̃X���ւ̌Œ胊���N�F http://5chb.net/r/math/1562421561/ �q���g�F http ://xxxx.5chb .net/xxxx �̂悤��b �����邾���ł����ŃX���ۑ��A�{���ł��܂��B
�����A�������P������낤����
�O�X��
������Ȃ����͂����ɏ����Ă�453
http://2chb.net/r/math/1558041041/ (�g�p�ςł�: 478)
�����͕�����Ȃ����������X���ł��B
�������������Ă���������ꏊ�ł��Ȃ�����
���R���̕��G�x�𗬍s�点����
���Ȃ݂ɁA�W��W(n)��W(1)��{1}�AW(2)��{1,2}�AW(3)��{1,2,3}�An��3�ɂ���
>>4 ��(n^k)��k��(n)�̔���
��(11)=8 ;11=(1+1)�~(1+1+1+1+1)+1
��(11^2)=15 ;11^2=(1+1)�~(1+1)�~(1+1)�~(1+1+1)�~(1+1+1+1+1)+1
>>6 ���Ⴀ�肪�Ƃ��������܂� ���݂�n��3�̂Ƃ��ɂ͐��藧���Ă��邱�Ƃ͏ؖ�����Ă��܂����w�Z�~�i�[�ɂ���܂���
>>5 �̒NjL�ł�
d��a����e��a-1�ł�
����ς蕔���ϕ�����Ȃ��B
��ϕ�I[x] = ��[1 to x] 1/{xln(x)} dx �ɑ��A
I[x] = ��[1 to x] 1/{xln(x)} dx =
>>9 h(r,��) = 2(1 - r�cos��),
�������
v/2 = ��[0�`1] ��[0�`60�] h(r,��) d�� rdr
�@= ��[0�`1] ��[0�`��/3] 2(1-r�cos��) d�� rdr
�@= ��[0�`1] 2r dr���[0�`��/3] d�� - ��[0�`1] rr dr���[0�`��/3] 2cos�� d��
�@= (��/3) - (1/3)[ 2sin�� ](0����/3)
�@= (��-��3)/3,
�����ϕ����Ȃ��Ă��o��B
>>10 J[x] = ��[e to x] 1/{x�ln(x)} dx = [ ln(ln(x)) ](e to x) = ln(ln(x)),
�͎����B
�����`ABCD�iAB<AD�j�̓��p��A��2��������L�Ƃ���B
((2n-k)!2^k)/(2n)!�@�ɍ������݂��Ȃ��̂͂Ȃ��H
�X���`�������炷�݂܂���B
����܋�������l�Ȃ����������W���_�Ɋւ��ċ����Ă���
>>21 ����X�����p���Ă�����I�W���_�̌������琳�������݂��ۏ���Ă邩�m�F��������B
>>22 ���肪�Ƃ��B����ς肻�ꂵ���Ȃ���
��W�������Ȃ��Ƃ���W�����܂ނ��Ƃ��������OK�Ƃ����������֗��Ȃ̂�����悩�������B
�����ɖ߂�̂͑�ςȂ̂ŁA��发���瑶�ݏؖ�������Ă���W���̒藝��T���Ă݂��
>>13 �n���P�����́A�~���g�i�܂���2������Ԃ̔g�j��\�킷���ł���A�����^�O���ɓ`������g��\�킷�B
>>25 ���肪�Ƃ��������܂��B
�����A�~���g��\���ƌ����Ă��A���̌`�łȂ��g�H�ƂȂ�̂ł����B
�x�b�Z�����ƃm�C�}�����̐��`�����������̂��n���P�����̂͂��ł������������Ȃ��A�n���P�����������̂��ƁB
�O
>>9 >>12 1-rcos�Ƃ��ǂ����킩��킩��Ǝv����ł��B
1-rcos�Ƃ�1�͒P�ʉ~�̔��a�ł����H
rcos�Ƃ͒��S���狗��r�̒n�_�̒��S����̋����ł����H
�����1��������Ƃ������Ƃ́A
1-rcos�Ƃ͒��S����r�A��`�̒[����Ƃ̒n�_�̒P�ʉ~���ォ��̋����ł����B
�����2�{���āA
2(1-rcos��)�͍����ł����H�@�܂荂��1�̒P�ʉ~�������l�ʑ�PABC�̑��ʂŊO�ɍ����ꂽ���g�O�̍����B
�ł��f�ʂ�1:2:��5�̒��p�O�p�`�ɂȂ�̂̓�=��/3�̂Ƃ������̂͂��B
h(r,��)�̒n�_��2�{���Ă�̂͂Ȃ��ł��傤�H
f(x)=3xx /(2xx +1)�Ƃ���B
0<a≤b�A0<R�A�Ƃ���B
�����ɂ��Ă̎���ł�
>>30 ���ؒ厡�搶����͊T�_�ł��̋L���͊���Z�Ə����Ă��܂�
�����ʂɑ�������ʂ̕ω������Ă���̂��{�`�Ȃ̂Ŏ��ۖ{���I�Ӗ��͊���Z�ł�
A��0�łȂ��萔�̂Ƃ��A
>>26 �Ȃ��g���H �����
2�����g��������:
�@{ (��x)^2+(��y)^2 - (��ct)^2 } �� = { r^2.(��r)^2+ r.(��r) + (1/r).(�݃�) + k^2 } �� = 0
�@�� �� exp(-i��t),�@k=��/c
���̈�ʉ�(�ɍ��W�\��) ��
�@��(r,��,t) = �� ( a[n]. J_n(kr)+ b[n]. Y_n(kr) ). exp(in��). exp(-i��t) �@
�̂悤�ɕ\���邩��ł��B
J_n, Y_n �͒��g (
https://imgur.com/a/CKaxlNo )
H1_n = J_n + i Y_n �͊O�����i�s�g (
https://imgur.com/a/Lrq5Lua )
H2_n = J_n - i Y_n �͓������i�s�g�ɂȂ��Ă��܂��B
���܂� (
https://imgur.com/a/YPSIGd0 )
3�����g���������̏ꍇ
�@{ (��x)^2+(��y)^2+(��z)^2 - (��ct)^2 } �� = { r^2.(��r)^2+ r.(��r) + (1/r)(�݃�) + k^2 } �� = 0
�@�� �� exp(ihz).exp(-i��t),�@k^2 = (��/c)^2 - h^2
��ʉ�(�~�����W�\��): �� = ��(r, ��,z, t) = (��)
�ƁA�܂� 2�����ɍ��W�Ƃقړ��������ɂȂ�܂���
k^2 < 0 �ɂȂ�ꍇ�͕ό`�x�b�Z���������ƂȂ�܂�. (���� I_n, K_n �ŕ\����)
����
>>30 �L�����Ӗ����̂��̂ł͂Ȃ��Ƃ͊m���Ȃ��ƂȂ�ł����ǁA���������ϕ��̗��j�̒��ł��������\�L�������c���Ă����̂ɂ͂�͂藝�R�������ł���
�����ƍl���Ă��ǂ��̂ł���
�lj�
Y_n �̒��g (
https://imgur.com/a/LoX4UdK )
plot �� python ��matplotlib ���g�p�����B
�ق��40�s���炢�� 3�����v���b�g, latex�`���Ń^�C�g������, gif �A�j�������܂ł���Ă��ꂽ�B
>>30 ���Z�����낤����[���˂����ޕK�v�͂Ȃ����ǁA�����`���Ƃ������̂��l�����dy��dx�Ȃǂ�P�Ƃň������Ƃ��ł��܂�
�ŁA�|�A���J���̕��Ƃ�������(�̓���ȏꍇ)����K���ȗ̈���dy=F(x)dx�ƂȂ��F�����݂��邱�Ƃ��m���Ă��܂�
���ۂɂ͂��̊�F(x)������dy/dx�ł�����A���̋L��dy/dx���udy=F(x)dx��dx�Ŋ��������́A�܂芄��Z�v�ƌ��č����x������܂���
����Ŕ���������Z�Ƃ��đ�����Ƃ܂����ꍇ������܂����A����͕Δ���(���ϐ����̊e�ϐ��Ɋւ������)�Ƃ������̂ŕ�������ɂȂ�Ǝv���܂�
>>30 ������̂͂����̃j�[���j�b�N�ŁA���ۂɂ͒u���ϕ����������������
����Z�Ƃ������Ƃ��͖Y���
>>4 ��(p)����(p-1)+1 �̍ŏ��̔���� p=353942783 �ł���炵��
�Ē���
>>32 �@-(1+x)�e^{-(1+x)} = -1/(Ae),
���
�@-(1+x) = W{-1/(Ae)},
�@x = -W{-1/(Ae)} -1,
�@W �� Lambert ��W�����B
2^n (n=1,2,3,...)�̈ꌅ�ڂ̐���2,4,8,6�̎����S�ŕω�����B
�����Œ肵��������I�Ȃ͓̂�����O������
���z�͌���ł��邯�ǂˁB
>>28 >>48 ���肪�Ƃ��������܂��I
�����25���ȓ��ɂ��̊�����������悤�ɂ��邽�߂ɂ́A�ǂ������v�l�̓���H��Ɨǂ��Ǝv���܂����H
>>49 ���z�Ƃ��Ă͋Ɍ��l���O���t�̌�_���琄�����鎞�Ɠ���
���Ƃ����_�q���鎮�ό`������
���ϒl�̒藝�����Ȃ�A�i�K�v�Ȃ�j�ŏ��̉��������Ԉ����ĕ��ϒl�̒藝���g���Ƃ���
���������B
�E�G���Z�łł���l�ɂ̂������ēK���������������̃��J�������\����ȁB
������ 0<z<1�Aa(1)=z �Ǝw�肳��Ă邼�Â�����n�Q
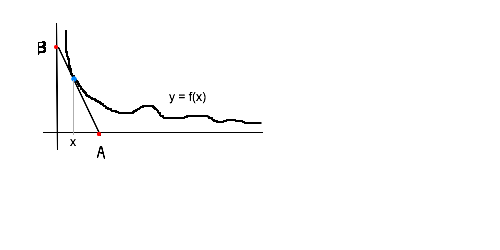
��������f'(x)=1�̉���0.19221�c��0.74767�c������Ȃ�
�O���t�`���Έ�ڗđR����[��A�I���B
�Ƃ��������ǁA���ꂶ��_���Ȃ�ł���ˁB
�ǂ������炢���̂�������ǁA
���̎�́u��ڗđR�v��I�Ɉ����ɂ͂ǂ������炢���̂��ˁH
����A
>>48 �݂����ȍH�v�����Ȃ��Ƃ����Ȃ��́H
�܂�1�����̐��̐�r��I�ԁB
>>57 ���ꎎ���ɏ����Ă����_�͂��炦�Ȃ��Ƃ���Ă�悤�ł��ˁB�����_�͂����ł��傤���B
����������Łc���[��c
�ǂ����������Ő�������Ί����ɂȂ��ł��傤�ˁH
>>40 ���Ⴀ�肪�Ƃ��������܂��B �����ł������B���ǑS���̗\�z���O��ĂĎc�O�ł�
�ł����G�x�͌��\�ʔ����̂ŊF������l���Ă݂ẮH
>>27 �@h �� ����PBC (���O�p��PABC�̈��) �̍����ł��B
�@(x,y) ���W�ł� h = 2(1+y) �ł��B(y=0 �� 2, y=-1 �� 0 ������)
�@(r,��) ���W�ł� h = 2(1-r�cos��) �ł��B
>>59 0<|z|<1/2�̎�
��Q����0<x<1/2
r=a(2)�Ƃ�����2�ȏ��n��(a(n),a(n+1))�͗̈�0<x<1�A|y|<|rx|
�ȉ�ry
1/2<|z|<1�̎�
��Q����1/2<x<1
r=|a(2)-1|�Ƃ�����2�ȏ��n��(a(n),a(n+1))�͗�1/2<x<1�A|y-1|��r|x-1|
�ȉ�ry
|z|>1/2�̎�
��Q����1/2<x<1
r=f'(1)�Ƃ�����2�ȏ��n��(a(n),a(n+1))�͗�1/2<x<1�A|y-1|��r|x-1|
�ȉ�ry
�i1�j���� 3^n = k^2 - 40 �������R���̑g(n,k)��S�ċ��߂�B
>>28 �̃^�C�v�̖��� ����I�Ɉ������A�����l���Ă݂�
y=f(x) �͒P�������ȘA�����Ƃ���
��1�@a[1] < f( a[1] ) = a[2] �̏ꍇ
�J��ԑ� S := { (a[1],t) ; x �� (a[1],t) �� x < f(x) }
������� U:= �� S = (a[1], q)�@(��L�E�Ȃ� q=+��)
�� := f(q)
�Ƃ���B
�A�����ɂ��, �C�ӂ̃�(>0) �ɑ� ��(>0)�����݂��� |��-q|���� �� |f(��)-��|����
U�̒�`���A����тɂ��� q<��<q+�� ���� f(��) �� �� (�P��������� f(��)=�� �ł���)
��-�� �� f(��) = �� < q+�� �� f(q+��) �� ��+��
�Á�0 �ɂ�� q=�� ��������.
(��̓I�� ���̓O���t�Ō�_�����߂āA������ U�̐����������������悢 )
��1.1�@ a[n]��U ���� a[n+1] not�� U �ƂȂ� n �����݂���ꍇ
����тɂ��� a[n] < �� �� a[n+1] ���� ��=f(��) (�撆�Ԓl�̒藝)
a[n] < �� �� a[n+1]=f(a[n]) �� f(��)=�� (��P������)
����� a[n+1]=��
���̒�`��� ������ , �P��������� ��=f(a[n]) �� f(��)=�� ����� ��=��
��=a[n+1] = f(��) = ff(��) = f...f(��)
�܂� lim a[n]=��
��1.2�@a[n]��U ���� a[n+1] not�� U �ƂȂ� n �����݂��Ȃ��ꍇ
a[1] < a[2] < ... < �� �ł���B
lim a[n] = �� �� �� (��ɗL�E�̏ꍇ) �Ƃ���. (�������Ȃ���� lim a[n]= +�� = �� �ł���)
�C�ӂ̃�(>0) �ɑ� ���� N �����݂��� n>N �� ��-�� < a[n]<a[n+1]=f(a[n]) < ��
����� lim{ f(a[n]) - a[n] }= f(��) - �� = 0, �O�Ɠ��l�̘_�@�� ��=��
�܂� lim a[n]=��
��2�@a[1] > f( a[1] ) = a[2] �̏ꍇ
1�Ɠ��l�̘_�@�ŏ���
��3�@a[1] = f( a[1] ) = a[2] �̏ꍇ
���炩
AB=1�AAD=a�̒����`ABCD�Ƒ����Ȓ����`PAQD������A5�_A,B,C,D,P�͓���~����ɂ���B
>>65 ����Ȑ}�`���蓾��H
AD�͒����`ABCD�̊O�ډ~�̒��a�ɂ͂Ȃ蓾�Ȃ�
P������~����ɂ���Ȃ��APD�͒��p�ɂ͂Ȃ蓾�Ȃ��̂�PAQD�Ƃ��������`�͍��Ȃ���H
>>64 > �A�����ɂ��, �C�ӂ̃�(>0) �ɑ� ��(>0)�����݂��� |��-q|���� �� |f(��)-��|���� ...
(�����͈ȉ��̂悤�ɕύX�\ )
�̓� �� (q-�� < �� < q) �� ( �� < f(��) )
q-�� < �� < f(��) �� f(q) = �� �� q �� ��
�̓� �� ( q �� �� < q+�� ) �� ( f(��) �� �� )
��= f(q)�� f(��)���� <q+�� �� �� �� q
����� �� = q
> ����тɂ��� a[n] < �� �� a[n+1] ���� ��=f(��) (�撆�Ԓl�̒藝) ...
(���Ԓl�̒藝�� �A���������g���Ă��邪�A�ȉ��̂悤�ɕύX�\)
��x �� (a[1],a[n] ) x < f(x)
a[n+1] not�� (a[1], �� ) ��� a[n]�� �� �� a[n+1]
f(��) = �� �� a[n+1] = f(a[n]) �� f(��) =��
����� a[n+1] = ��
�܂�O��́uy=f(x) �͒P�������v�����ł悢�B
�A�����A�����\���͕s�v
�ڍs���ā�������v���X�}�C�i�X�t�ɂȂ��ˁH
>>68 �������̊W������Ƃ��A
���ӂɓ��������⎮�𑫂��A�����A0�ȊO�̐���������A�Ȃǂ��Ă����ӃC�R�[���̊W�͂����Ɛ�������
�Ⴆ��
���{�R�����{�R
���{a����+a�ɂȂ�
�Ȃ̂�
b-a=3
��(���ӂ�a�𑫂�)
b=3+a
��(���ӂ���3������)
b-3=a
>>63 �����͂��܂����o��҂Ԃ��Ė����o���ꏊ����Ȃ����玸���득�������̃K�C�W
>>63 ���܂����̕a�C�����ė������Ă�H
�Ȃ�Ŏ��������N���������ɂ���ĂȂ��������ł���H
>>67 (����)
��1.2 �ɂāAlim a[n] = �� �� lim f(a[n]) = f(��) �܂�A�������g���Ă��܂��Ă���.
����ɂ悭�l���Ă݂��, �A���łȂ��Ȃ� �� ;= f(q) �� �� �� q �̏ꍇ������.
�Ȃ̂ŁA���������C�����K�v�����A����ł��A�����̑O��͊O����Ǝv���B
>>68 �E�ӂƍ��ӂ����ւ��邩�A�r���ǂ����ŗ��ӂ�-1���|��������Ȃ�
>>63 ���ʏ��n�in≥4�j�̓_������B
>>75 �����͂��Ȃ��������o���ꏊ�ł͂���܂���
���f�Ȃ̂ŏ������܂Ȃ��ł�������
����3�N
�Γ����̉��p
�ȉ�url�̕s���������t���ő�l�ŏ��l��肪������܂���B
���������藧���Ă���ȉ~��̓��O�����W���̖���搔�@�ŋ��܂�Ǝv���̂ł����A�ȉ~���̍ő�l�ŏ��l�̋��ߕ���������܂���B
��낵�����肢���܂��B
>>72 (����)
�A�����̑O����O����
�����������C�����������������ł��鎖������̂ŁA��߂��ق����悳�����B
���傤���Ȃ��lj��O�K�v�ɂȂ��Ă���B
>>78 x=2acos��cost
y=bsin��sint
x(x+y)-y^2=1
>>81 �Ȃ�ł��̐l����ȂɌ����Ă�́H
>>78 �͂����}�W���Ƃ����ڂ���܂�www
�A���藝�ɂ��Ď��₳���Ă��������B
f(x, y)=0�̂Ƃ��Ay�f=-fx/fy�Ƃ����藝�ł��B
�����j�X�P�[�g�Ȑ�4(x^2+y^2)^2-(x^2-y^2)=0(
)
�ɂ�����g���ƁA(x, y)=(0, 0), (�}��6/8, �}��2/8)�ɂ�y�f=0�ƂȂ邱�Ƃ��킩��܂��B�������A���ۂɂ�(0,0)�ł�y'=0�ł͂���܂���B�Ȃ����̂悤�Ȃ��Ƃ��N����̂ł��傤���H���̓_�́A�A���藝��K�p�ł�����������Ă��Ȃ��̂ł��傤���H
��낵�����肢���܂��B
�ɃɃ��Ƀ�������������
>>82 ���������ǂ͂ǂ��ł������邾��w
�X���̎g�������炩�ɊԈႦ�Ă����
���O�̈Ӗ��𗝉��ł��Ȃ�5ch�ɂ悭���铜���̓T�^��
>>69 ����͓����̐�����
��w�ȍ~�͓��l�W�Ő�������ׂ��ł���
>>86 �����Ǝ��ǃX�y�N�g�����͑S���ʂ̕a�������v���H
>>78 �Exyt��ԋȖ�: f(x,y,t) = xx/4 + yy + tt = 1 (t��0) ...(1)
�E���̖@���x�N�g��: (x/2, 2y, 2t )
�Exyt��ԕ���: x + y + t = z ...(2)
�E���̖@���x�N�g��: (1,1,1)
�� t �� 0
z���ɒl���Ƃ������ 2�̖@���x�N�g�������s�ɂȂ��Ă��鎖 (������̓��O�����W������搔�@���̂���)
(x/2, 2y, 2t ) = k*(1,1,1) {k:���W��}
(1)�ɑ������ 4kk/4 + kk/4 + kk/4 = 1 �� k = �}��(2/3)
z = x + y + t = 2k + k/2 + k/2 = 3k = �}��6
�� t = 0
�Exx/4 + yy = 1
�Ex + y = z
���x�� 2�����łœ��l�ɏ�������
(x/2, 2y) = k'*(1,1)
4k'k'/4 + k'k'/4 = 1 �� k' = �}2/��(5)
z = 2k' + k'/2 = (5/2)*k' = �}��5
����� +��6 ���ő�l, -��5 ���ŏ��l�ł���
�Ă�... �E��ɕΓ������Ƃ������Ă����ł�����...
���H��w���x���ł��������̃A���Ȃ́H
>>78 >>80 >>64 ���肪�Ƃ��������܂�
�������A������Ɨp�ꂪ����A�����ɂ͎���܂���ł���
���i���܂��B
>>81 �t�B�{�i�b�`���� F_n �Ƃ����B
�@G_n = F_n�{F_n + F_(n+1)} - {F_(n+1)}^2
�@= F_n�{2F_n + F_(n-1)} - {F_n + F_(n-1)}^2
�@= (F_n)^2 - F_(n-1)�{F_(n-1) + F_n}
�@= - G_(n-1)
�@= �����
�@= (-1)^(n-1)�EG_1
�@= (-1)^(n-1) {F_1�(F_1+F_2) - (F_2)^2}
�@= (-1)^(n-1),
���@(x, y) = (F_{2m-1}, F_{2m})�@�͑�ӂ����B(m�͎��R��)
m=10 �̂Ƃ��@(F_19, F_20) = (4181, 6765)
>>84 �@������̘A����
>>81 (x, y) = (1, 1) �͑�ӂ����B
(a+b){(a+b)+(a+2b)} - (a+2b)^2 = a(a+b) - b^2,
���@(x, y) = (a, b) ����ӂ����Ȃ�@(a+b, a+2b) ����ӂ����B(�I)
>>89 �Ȃ�ق�!
���̕��@�ʼn����ƃG���K���g�ł��ˁB
�킩��₷��������肪�Ƃ��������܂����B
�܂��@�����܂������낵�����肢���܂��B
���L�̂悤�Ȏ��͔��ϕ��̂ǂ���������ŏo�Ă���̂ł����H
�O
>>27 >>12 ���l�ʑ�PABC�ƒP�ʉ~�������𑫂����߂Ĉ����ꍇ�A�ǂ��������ɐ����f�ʐς��ǂ��������ɑ������߂܂����H
r�ƃƂ�2�̕ϐ�������ꍇ�A�ǂ����N�_�ɂ�(�ǂ���r=0,��=0�܂���0�����Ƃ�)�܂����H
�����m�Ɏ����Ύ��͐l���ꂼ�ꏟ��ɗ��Ăĉ����Ǝv����ł��B
���������ϕ��̓��Ăɂ́A�����ƋN�_�������Ă��������B
r=0 �͉~���̎� (z���AOP),
>>81 ss = Solve[x^2 + x y - y^2 == 1 , y];
n = 1;
Do[
If[IntegerQ[py = (y /. ss[[2]])], Print[{n++, x, py}]], {x, 0,
10000}]
{1,1,1}
{2,2,3}
{3,5,8}
{4,13,21}
{5,34,55}
{6,89,144}
{7,233,377}
{8,610,987}
{9,1597,2584}
{10,4181,6765}
�ŕЂ��t��
�ؖ��H�@�t�B�{�i�b�`�����R�łĂ��邪�A���������Ȃ��Ă��@�Ȃ�Ƃ��ł���ł��傤
1�T�ȏ�͌v�Z���Ԃ������肻������
0<��<��<90�Ƃ���B
�O
>>97 >>98 y���̕��̕�����r=cos�Ƃ��Ƃ����Ƃ������Ƃł����H
���w�̐V�����������Ǝv���̂ŏؖ��ȂǑ��낤�Ɠ��{���w��Ƀz�[���y�[�W�ɍs������
>>99 �C�J�������ꂾ��
wolfram? wolfram alpha?
Wolfram����̓v���b�g�t�H�[���ɍœK�����ꂽ
>>100 �� = �� + ��, b = a - ��' �ƒu��
�����藝��� a sin�� = b sin�� = (a - ��' )sin(�� + ��) = (a - ��' ){ sin�� + ��.cos�� + o(��^2) }
��' sin�� = a ��.cos�� - ��'��.cos�� + o(��^2)�@�� lim (��/��') = tan�� / a
{cos��-cos��}/(b^2-a^2) = {cos(�� + ��)-cos��}/{(2a - ��')(-��')} = sin��/(2a) * ��/��' + o(��^2)
= sin��/(2a) * tan�� /a + o(��^2)
�� sin�� tan�� /(2aa)
���₾������܂�����
���ɓ�����X���炵���̂�
>>81 (loop for x from 1 to 100000 do (loop for y from 1 to 100000 when (eq 1 (- (* x (+ x y)) (expt y 2))) do (format t "x:~a y:~a~%" x y)))
x:1 y:1
x:2 y:3
x:5 y:8
x:13 y:21
x:34 y:55
x:89 y:144
x:233 y:377
x:610 y:987
x:1597 y:2584
x:4181 y:6765
�����������e�͑�܂��ɂ�����
���ȏ���3���������ł̓J���_�[�m�A4���̓f�J���g�Ƃ��łĂ�������
�Ȃ�قǁA���x�̐f�@�̎��������葝�₵�Ă��炨����
��̊��S������݂����ɘ_���i�j���n�Q�U�炩���Ă݂���H
�O
>>101 >>98 �l�ʑ�PABC�͎O�p���ł͂Ȃ���ӂ����O�p�`�̎O�p���ł��ˁB
>>111 ������
>�N�����{���w��ւ̃A�N�Z�X�m��Ȃ��H
�Ȃ̂���
>>113 �Ƃ肠�����X�����ĂĂ݂���ǂ��ł��傤�B
���j�I�听�ʁH����������̊��S������ł���A�R�c�R�c��web�Ř_���n�Q�U�炩������
>>114 �����Ă��͐V�����Ȃ�Č���ŒN�������Ă�̂��I�`�����
>>107 ����m���Ă��@Xxx�������� Xxx �̒藝
�Ƃ����X�����͂�
���O��̂悤�ȖŒ��ꒃ���w�o������Ȃ�
�m����\��������
�O
>>112 >>98 �ǂ��������ɐ��Ăǂ��������ɑ������߂���A
���邢�͒��p�O�p���䂩��3�����ؓ��P�ʉ~����1/6�̂ǂ��������ɐ����f�ʐς��ǂ��������Ɉ������߂���A
���߂�̐ς�1/6�A
2��3/3-��/3
�ɂȂ邩���m�肽���ł��B
���O�̃f�t�H���g�ɂ��Ȃ��Ă���悤�ɁA�����f���D���݂���������
���y�Y�Ƃ��đf���W�F�l���[�^�̃R�[�h�u���Ă�����
https://pastebin.com/EEQkRR1W ���x�̏o����C����ŃL���b�V���w������3MB���������g��Ȃ�����
10000000000�����̑f���S�������o���R�[�h
�e�L�X�g�t�@�C���ɑS�o�͗������ނƖ�5GB���炢�ɂȂ�͂���
���x��1�b�Ԃ�1�����炢�f��������y�[�X������
���Ԃ���퐶���őf���\�������Ȃ�����1�b���炢�ŏ\���Ȃ�Ȃ��ł��傤��
�f�����炭���Ȃ��Ȃ�t�@�C�������ăR�[�h���������Ă���قڃt�@�C���T�C�Y0�ŕۑ�������
�K�v�Ȃ琔�M�K�o�C�g�Ƃ��o�͂��Ă����ΐF�X���ׂ�̂ɕ֗�����
�����̏Z����������������Ƃ������l�т����˂�
>>100 a,b ���萔�̏ꍇ
�@sin��/sin�� = sin(��A)/sin(��B) = PB / PA = b/a,
�@������ �Ƃł��邩�� �@a=b�H
a,b ���ϐ��̏ꍇ
�@PAB�̃T�C�Y�����R�ɕύX�ł���̂ŕs��H
t�������̒萔�Ƃ���B
>>118 �������点�Ă݂܂����B�@�����Ă͍���̂łP�O�O�O�O�ȉ��ɂ��܂������A
����ꂽ�ʂ�ł��B
C���g��Ȃ��Ȃ��ĂЂ������̂ł����A�̒ʂ��C�ʼn��������ł��B
���肪�Ƃ��������܂����B
>>101 �@y���̕��̕��� (��BOC�̒����̕���) �� ��=0 �����܂����B
a,��,���𐳂̒萔�Ƃ���B
�����l�W�ł͂Ȃ�
>>124 ���̃X���͂��Ȃ����N�C�Y���o���X������Ȃ�
p ���U�̎��A p �� q �͐^�ɂȂ�܂��B
p ���U�̎��A p �� q �͐^
�Ƃ����͂����P�ɕ֗������炻������܂ł�
�Ɩ{�ɂ͏����Ă���܂��B
>>128 ��W���͔C�ӂ̏W���̕����W���ł��邱�Ƃ��ؖ��ł����肵�āA�m���ɕ֗��ł��B
>>128 �̗�ȊO�ŁA���̖��֗��ȏ�ʂ��Ă���܂����H
p
p(x) �� q(x)
��
�����āA
���ۂɐ��w�̖{��ǂ�ł��Ă��A
��̓I�ɁA���鐔�w�I�c�_�̒��ŁA
True �� True == True
����̐^�U�ɂ��ċ^�₪����̂Ȃ�
��`���ؖ�����Ƃ����ْ͈̂[�̂悤�Ɏv��ꂪ������
>>105 �� o(��^2) �� �������Ƃ��� o(��) �ɒ�������
lim{�� 0} o(��) / �� �� 0 �ƂȂ�悤�Ȕ����� (�����_�E�L�@)
>96
����ł��B210/ 5.5���v�Z������x��38��10/55 �ɂȂ�܂����B����͂ǂ��v�Z�����ł��傤���H�l���������38��2/11�ɂȂ��Ă��܂��܂��B
>>141 �����������܂����B2100/55�Ōv�Z�����炻���Ȃ�܂��B�Ȃ��A420/11�Ŗł���̂ɂ��Ȃ���ł��傤���H
�ڂ����������������储�̂Ƃ������������Ă݂�H
>>141 >>142 ���ȉ������܂���
m,n�����R���Ƃ���B
>>145 ����
a[m,n]���ŏ��ɂ��遨|a[m,n]|���ŏ��ɂ���
>>136 ���肪�Ƃ��������܂��B
�ǂ�ł݂܂��B
>>145 log(6)/log(2) = 2.5849625
{log(6)/log(2)}^2 = 6.68203113
���
�@m �� 6
a[4,2] =�@0.0076122315315
a[5,7] = -0.0593537672425
a[5,8] =�@0.0155611898880
a[6,53] = -0.0006100055500
a[6,54] =�@0.00063278544533
(m,n) = (6,53) �̂Ƃ��ŏ��B
>>145 a[m,n] = log_2[6] - (��m + 1/��(n+1))
���킩��₷��������Â��Ă������B
a[m,n] = log_2[6] - (m + 1/��(n+1))^(1/2)
a[m,n] = log_2[6] - (m^1/2 + 1/��(n+1))
or
....
�@F(n,s) := ��{k=0, n} C{n,k} * (-1)^k * (n-2*k)^s
(�⑫����)
>>151 ���ȉ������܂���
F(n,s) := ��{k=0, n} C{n,k} * (-1)^k * (n-2*k)^s (s=0,1,...,n-1)
�Ek �ɂ��Ă̑�����: (n-2k)^s �̎����� n-1 �ȉ��ł���
�E��{k=0, n} C{n,k} * (-1)^k * k^t (t = 0,1..., n-1)
�@= ��{k=0, n} C{n,k} * (-1)^k * (d/d��)^t e^{k��}�@ (����0)
�@=(d/d��)^t ��{k=0, n} C{n,k} * (- e^{��} )^k�@ (����0)
�@=(d/d��)^t (1-e^{��})^n�@ (����0)
�@=(d/d��)^t (1-e^{��}).... (1-e^{��}) �@(����0)
�@= 0 (�� t < n)
����� F(n,s) = 0 (s=0,1,...,n-1) �ł���B
��ӂ��炢�Y�̂ɈӊO�ƊȒP�������B
���ł� F(n,n) �̎������܂����B
F(n,n) := ��{k=0, n} C{n,k} * (-1)^k * (n-2*k)^n
= (-2)^n * ��{k=0, n} C{n,k} * (-1)^k * k^n
= (-2)^n * (d/d��)^n (1-e^{��}).... (1-e^{��}) �@(����0)
= (-2)^n * n! * (-e^{��})...(-e^{��}) �@(����0)
= 2^n * n!
�O>>149 �ǂ��������H __�l�l__
/__�l�l__/__/�i__^_)_
/_(__)_)_/__/�i____)_
/_( ___)_/__/�i^o^))_
/_(_�i`)_/__/_(__����
/_(��__)��__��ބ��ҁ��
��ރ҄�-���_/__/�����c�c/__/__/_�����c�c__/__/__/__/�O
>>154 ����ς�
>>12 �̂悤�ɉ��������Ȃ����B
log[(x^2)�{2]��0�����2�܂�x�Őϕ����Ă�������
>>156 log[(x^2)�{2] = log(x + i��2) + log(x - i��2) ���
�s��ϕ�: �� dx log[(x^2)�{2] = (x + i��2)log(x + i��2) - (x + i��2) + (x - i��2)log(x - i��2) - (x - i��2)
= x log(x^2 + 2) + i��2 log[(x + i��2)/(x - i��2)] - 2x
= x log(x^2 + 2) - 2��2 arctan[ (��2) / x ] - 2x (�����o�ߒ����������v���Ȃ�R����������Ċm���߂�Ƃ悢)
���Ƃ͐��l�����邾��
sample
�R�s�y�݂�
>>160 ���߂ĕ������[�h��
>158
�Ɍ����ڂ�������H
>>160 ���Ă��邪�Ⴄ
�������������� i j ��F�����Ă��邪 k��F���ł��ĂȂ�
������
ij = k �ƂȂ��Ă��邪
�����̌������@���ł�k�Ɉڂ�Ȃ�
���Ƃ��� j ���̃f�[�^�̃��[�g�̒���������
����i �ŕ\�킹�邯��
�^�h���A�u���̒藝���g���ƕ��f������(�F���g�� �����Ƌ���i�̍��W)
�ɕϊ������B�f����k�ł͂Ȃ�
wiki �ɎO���� ������
�O�����̓n�~���g�����v�Z���ςɂȂ���ĔY����ȁB�B
�O�����Ɩ�������̂�߂�
>>158 >>159 ���܂܂ł̒�Ԃ���1�̎�������a�Ƃ�����
����2�̉���k �܂����ˁH
���̂�a�ŕ\�L�ł��܂�
������
�J���_�[�m�̓�����̂悤�ȓ����3�捪������Ȃ�
>>12 �l�ʑ�PABC-(1/2)^3�l�ʑ�PABC-6(�l�ʑ̓���������o��0��z��1,0�����Ɓ�60���̕���)
=2��3(7/8)-6(��-��3)/3
=7��3/4-2��+2��3
=15��3/4-2��
�ŏ���2��3-6(��-��3)/3
=4��3-2���Ǝv������ł����A(��-��3)/3��6���o�����̗��̂́A0��z��1���Ǝl�ʑ�PABC��1/8�͏��O����̐�(2��3)(7/8)=7��3/4�̎O�p����ɂȂ��Ȃ��ł��傤���H�@ �O
>>155 �O
>>167 ����Ƃ�
>>12 �́A
v/2=��[0�`1]��[0�`60�]h(r,��)d��rdr
=��[0�`1]��[0�`��/3]2(1-rcos��)d��rdr
=��[0�`1]2rdr��[0�`��/3]d��-��[0�`1]r^2dr��[0�`��/3]2cos��d��
=(��/3)-(1/3)[2sin��](0����/3)
=(��-��3)/3
��OB���ΕӂƂ��钼�p�O�p�`(��OBC�̔���)���ӂƂ���O�p���̒��_P���܂ޑ̐ςł����H
t�𐳂̎����Ƃ���B
>>169 ���f������X�����������S�~
>>169 ���̃X���͂킩��Ȃ����������X���ł����̖₢�̓��ɉ���������Ȃ���ł����H
>>169 �����̃��X�Ƒ��̐l�̃��X�ʼn����Ⴄ�Ǝv��Ȃ��H�v��Ȃ��Ȃ炠�Ȃ��͓���
>>151 >>153 �������ς��� >>156 �����ϕ���
�� log(xx+2) dx = x�log(xx+2) - �� 2xx/(xx+2) dx
�@= x�log(xx+2) + ��{4/(xx+2) -2} dx
�@= x�log(xx+2) + (2��2)��1/(tt+1) dt -2x
�@= x�log(xx+2) + (2��2)arctan(t) -2x
�@= x�log(xx+2) + (2��2)arctan(x/��2) -2x,
0����2 �Őϕ������
�@(2��2){log(2) + ��/4 -1} = 1.35353063127
>>159 >>166 �@�u1�̎�������a�Ƃ���Ƃ��A����2�̉���a�ŕ\�L����B�v
�Ȃ�
�@b+c = -a,
�@bc = aa -13,
����⏕������
�@tt + at + aa -13 = 0,
�����������
�@b, c = {-a �} ��(52-3aa)}/2,
1����99�܂ł̐���N�ŁA|sinN|���ŏ��ɂ�����̂����߂�B
�ނ���
{Pi+2m Pi,{m,1,15}}
>>178 1/(2��) ���������Ȃ̂� ���f���ʏ�� z=e^{ik}=e^{i2��* (k/(2��))} k=1,2,3,.... ���v���b�g����� �P�ʉ~���f���ɕ����s�����B(�N���l�b�J�[���f���藝��薾�炩)
���� z= -i �̔C�ӂ̃ËߖT�ɂ�����ł��U����Ă���B
�܂� �̓� ��k |sin(k) - (-1)| = | Im(z - (-i)) | �� | z - (-i) | < ��
����� lim�on �����pa[n] = -1
Integrate[Log[x^2] + 2, {x, 0, Sqrt[2]}]
>>156 >>175 �Q�l��
�X���E�F�c��E�ꏼ�u���w����I�v��g�S��221 (1956)
�@p.167 ��20�\�@�h[n] = ��(x^n)log(xx+c) dx
>>181 �Ђ���Ƃ��ĘA�����W�J�Ɉ˂炸���l�v�Z���܂������H
>>177 �@sin(11) = -0.999990206550703
�@sin(55) = -0.999755173358620
�@sin(99) = -0.999206834186354
�̂ǂꂩ�B
>>178 �@f(i) = i - 2��[i/2��]
�Ƃ�����
�@0 �� f(i) < 2��
�@f(0), f(1), f(2), ����, f(m) ��(m+1)�̒��̈��� i��j �ɂ���
�@0 < |f(i) - f(j)| < 2��/m,
�@n �� |i-j| �����������Ƃ��� f(n) �̕ω��� 2��/m ��菬�����B
�@�C�ӂ� ��>0 ���Ƃ��ā@m = [��/��(2��)] + 1 �Ƃ����B
�@|f(i) - f(j)| < 2��(2��),
�@n �� |i-j| �����������Ƃ��� f(n) �̕ω��� 2��(2��) ��菬�����B
�@���� f(n) �͋�� [ -(��/2)-��(2��), -(��/2)+��(2��)] �̒��ɓ���B
�@sin(n) = sin(f(n)) < sin(-(��/2)�}��(2��)) = -1 + 2{sin��(��/2)}^2 < -1 + ��,
>>187 ������Ƃ������������傤���傤�̃K�C�W
t�������̒萔�Ƃ���B
>>191 ���f�����珑�����܂Ȃ��ł�������
>>191 �����ĂȂ��A�s�[�����Ȃ��ėǂ�����
���܂��̂����ł݂�Ȃ����f������
>>187 >>186 ������Ȃ����������X���Ȃ̂ɂȂ�œ����m���Ă�����������́H
�O�w F �̑w���Ƃ͑w [F] �Ə����^ f: F��[F] �ł����āA���̕��Ր��������̂ł�:
>>196 G=[F]�Ƃ����g��f��ϊ����Ă����h�����݂���킯������
���^�������Ĉ�ӂ���Ȃ��́H
�����ڂ�2�����̖��Ȃ̂ɓ��B����܂��H
���O�]�T�Ȑl�ł��Ȃ�������ޑ�w�̓��Ȃ�Ă����ς����邾��
���A�K�C�W�Ƀ��X���Ă���
�R�[�V�[���[�}���̕������Ł�u/��x=��v/��y
�u➀�Ƃ���v��������➀�����藧�Ɍ��܂��Ƃ邾��
>>201 z = x + iy , f(z) := F(x,y) = u(x,y) + i v(x,y)
�R�[�V�[���[�}�������ɂ�� f(z) �� D�Ő����ł���B
��^2u/��x^2 = ��^2v/��x��y = ��^2v/��y��x = -��^2u/��y^2 �� ��u = 0
��^2v/��x^2 = -��^2u/��x��y = -��^2u/��y��x = -��^2v/��y^2 �� ��v = 0
g(z) := U + iV = ��u/��x + i ��v/��x ( = ��v/��y - i ��u/��y ) �Ƃ���ƁA
��U/��x = ��^2u/��x^2 = -��^2u/��y^2 = ��V/��y
��U/��y = ��^2v/��y^2 = -��^2v/��x^2 = -��V/��y �܂�R�[�V�[���[�}����������������B
����� g(z) ���܂������ł���A��U = ��V = 0 �ł���B ( ���߂Ă����̂͂���ŗǂ��H)
���āA��z = ��r.e^{i��} = ��r.cos�� + i ��r.sin�� = ��x + i��y �ƒu����
��f/��z := { (f(z+��z) - f(z))/ ��r }. e^{-i��}
= { (��u/��x+i��v/��x).cos�� + (��u/��y+i��v/��y).sin�� }. e^{-i��} + o(��r)
= { (��u/��x+i��v/��x).cos�� + (-��v/��x+i��u/��x).sin�� }. e^{-i��} + o(��r)
= { (��u/��x + i��v/��x).(cos�� + i.sin��) }. e^{-i��} + o(��r)
= ��u/��x + i��v/��x + o(��r) = g(z) + o(��r)
����� g(z) = f�f(z) �ł���B
>>202 �������̗��ӂ�Δ����������͕̂������ɂȂ�̂��Ƃ������Ƃł�
�O
>>168 ���K�B
�l�ʑ�PABC=2��3
���̂����~������
x^2+y^2��1
��1/6�́A
��[0��1][0����/3]2(1-rcos��)rdrd��
=��[0��1][0����/3]2rdr��-��[0��1][0����/3]2r^2cos��drd��
=1�(��/3)-(2/3)sin(��/3)
=��/3-��3/3
=(��-��3)/3
���߂�̐�=2��3-6{(��-��3)/3}
=4��3-2��
�ȂɁHx=y�̂Ƃ��Ɏʑ�f�Ŏʂ���f(x)=f(y)�����藧�̂����Ă��ƁH�H�H
�����͂��ĂȂ�����{�I�ɒ��ւ̎ʑ������藧�Ƃ����O��ŋc�_�����Ă���
>>203 2,3�i�����������Ă���̂��킩��Ȃ��̂ł����A��u/��x=��v/��y�Ȃ��
��^2u/��x^2=��^2v/��y��x�ɂȂ�Ƃ������Ƃł����ł����H
>>204 �������Ƃ��Ȃ��͌����Ă܂����A�ȂɂɊւ���ǂ̂悤�ȕ������ł����H
���ꂪ�͂����肷��킩��͂��ł���
�킩��Ȃ������Ă킯�ł��Ȃ���ł������������܂��B
>>157 >>175 ���肪�Ƃ��������܂���
�P���ȃ~�X���������ǂǂ������炢���H�̊|���Z�ł���������~�X�������B
�݂��ɑf�Ȏ��R��a,b,c�͓���
�L���Ȃ�ʏ��abc�\�z����������ΐ������B
lim[n=1����](-1)^n/n^2
���ƁA(-k)^n/n! (k>0)�̖����a�́A
>>215 �}�W���X���Ƃ���
�P���v�Z�́A2��v�Z���Čv�Z�������ʂ��������Ƃ��m���߂�B
���x���v�Z�~�X���Ă��邤���Ɍv�Z�~�X������ꏊ����̂킩���Ă��邩��
�����Ɋւ��Ă����ł�2��v�Z����
���w���p�̃h�����œ��~���̖��ł�����20��ʂ���Ă���
>>215 2�����(�{�����邪��I�ȃG���[���o)
�T�Z(��܂��ȃG���[���o)
mod10(�ԈႢ��1�̈ʂɏW�����Ă���Ȃ炱��͂Ȃ��Ȃ�)
...(�����Ɛ��x�̃g���[�h�I�t�̉���)
>>218 ��[n=1,��](-1)^n/n^2 =-(1/2)��(2)= -��^2/12 : ���Z���w�ʼn\�A�����L�[���[�h�u�o�[�[�����v
��[n=1,��](-1)^n/n^3 = -(3/4)��(3) : ���[�}���[�[�^����(s)�̒�`��m���Ă�����Z���w�ʼn\
��[n=0,��](-1)^n/(n!)^2 = J0(2) : �x�b�Z����Jn(x)�̒�`��m���Ă�����Z���w�ʼn\
�u���Z���w�ʼn\�v �̒�`�K�o�K�o�����ł�...
>>213 ��������
www.mathnet.ru/eng/rm8256
>>222 ���[�ށc
���߂܂���
�����Ă���Ă��肪�Ƃ�
�݂��ɑf�Ȏ��R��a,b,c�͓���
>>227 ����
c=2^N, 3<=N�Ƃ���
a, b �̂ǂ��炩���������Ȃ��
�^���͂˂ɐ��藧��
>>229 �K�C�W�Ƀ}�W���X�����
��ӂ̒�������2�̐����`ABCD�̎��y�ѓ����̗̈��S�Ƃ���B
>>231 �ӊO�ȋȐ��ƁA�ӊO�Ȗʐς̒l���o�Ă��܂��B
>>232 �X���^�C���ǂ߂Ȃ��̂ɂ悭���{�ꂩ������
�R�s�y�H
���_����c���Ɍ��˂��A�_(0,1)�Ŕ��˂��ĉ����ƌ����_��X�Ƃ���
�C�ӂ̐��̎���a�ɑ��A
f, g ����,x ���X�ɂ��Ă̖��x���Ƃ����
f(��) d�� = g(x) dx �����藧���Ă��܂��B
�z�u������� x = tan��
d��/dx = 1/{dx/d��} = (cos��)^2 = 1/( 1 + xx )
f(��) �� -��/2 �� �� �� +��/2 ���Ȃ̂� f(��) = 1/��
����� g(x) = f(��) d��/dx = 1/ {��.( 1 + xx )}
>>234 �⑫����
> f(��) d�� = g(x) dx �����藧���Ă��܂�
�܂� ��[��=a,b] f(��) d�� = ��[x=��(a),��(b)] g(x) dx �Ƃ������ŁA
���ꂪ������̂� x = tan�� [��:-��/2, +��/2] �̂悤�� x �� �� ����ΊW�̏ꍇ�݂̂ł��鎖�ɒ��ӂ���K�v������܂��B
��Έ�łȂ����͑����̏����������K�v�ł��B
����: ��[��=a,b] f(��) d�� = ��[x=x(a),x(b)] g(x) dx
x,y �͐���
�Ȃ�Ŗ������ɂ��������Ă�̂���ˁ[��
n>=6 ,x,y,z �͎��R���̂Ƃ�
�����Q�P�T
���R��n��10�i�@�\�L�����Ƃ��̐擪�̐�����a[n]�A�����̐�����b[n]�Ac[n]=10a[n]+b[n]�Ƃ���B
>>236 ���P
exp(xx) > 1+xx ���
(�^��) < ��[0,a] 1/(1+xx)^2 dx
�@= (1/2)a/(1+aa) + (1/2)arctan(a)
�@< ��/4
�@= 0.7853981634
���Q
GM-AM ���@exp(-xx)/(1+xx) < {1/(1+xx)^2 + exp(-2xx)}/2,
(�^��) < (1/4)a/(1+aa) + (1/4)arctan(a) + (1/8)��(2��)erf((��2)a)
�@< {�� + ��(2��)}/8
�@= 0.706027616
�Ȃ��A�^�l�� (e��/2)�erfc(1) = 0.67164671
�C�ӂ�n�̎���x1,x2,x3,�c,xn�ɑ��āA
�������ċC�Â����̂ł���n=1�Ŋ��Ɉ�ӂɒ�܂�Ȃ������ˁc�����܂���
�A�������܂���
�����X���̃��x���𑪂�����Ł[ ���ăm���Ȃ�ˁB ���l������Ęb�B
�v���Ă�����ǁH
�����Ȃ��Ă������Ə����Ă邫�������j�[�g�Ȃ��疳�����Ƃ���������
�ł������Ă�z���������Ɏ��������̃X���Ō��������Ƃ͎v���ĂȂ��C�͂��邯�ǂˁB
�����͂悭���̃X���ɐ��b�ɂȂ��Ă���������ˁA����Ȃ�Ɉ�������킯��B
���ɂ���A�����킩���Ă�����������s�ׂ̓X���`����Ȃ��̂����H
�X���`�ł��邱�ƂɈ٘_�����͂��Ȃ�����
�X���`�����r�炵�����ǍU�����Ă������N�����Ƃ͎v��
���肪�^�Ȃ̂�������Ȃ��̂ł����A��ԉ��̍s�̖���̏ؖ��������ĉ�����
��͗͊w�̃��O�����W���������̓��o�ŕK�v�ɂȂ������ł�
�ǂ݂ɂ����Ă��݂܂���낵�����肢���܂�
���炵�܂��B
�d�ϕ����Ă��Ƃ�2�ϐ���z=f(x,y)���Ǝv�����ǁc�cx��y�������ł���
>>262 �Ȃ�Ƃ������c
x�Őϕ�����Ƃ������Ƃ�xy���ʏ�őсH���W�߂ĕ��ʂ̖ʐς��o��C���[�W�Ȃ�ł���
���̂���y�Őϕ�����ƂȂ�Ƃ�����x�����悤�ɖʐς��o���Ă��銴���ōl���Ă��܂��B�������ɊԈႦ�Ă���悤�ȋC�����܂����c
���܂������ł��Ȃ��Ă��݂܂���B
>>260 �Ō�̎��̎������炵�ĉ����ςł����
�{���͉��̌v�Z�����Ă��ł����H
>>263 https://www.geisya.or.jp/ ~mwm48961/electro/multi_integral3.htm
�K���ɃO�O������o�Ă��܂���
dxdy�Őϕ�������Ċ����ł�����
>>265 ���肪�Ƃ��������܂��B
�Ƃ�ł��Ȃ���������Ă������Ƃ��킩��܂����B
����ƃC���[�W�ł��܂����B
>>261 ������Ɗ��S�ȋ��̂̑̐όv�Z���܂��傤
����Ȃ�ڂŌ����邵���������m
>>267 �킩��܂����B
����Ă݂܂��B
�����Ă��������������肪�Ƃ��������܂����I
��[k=0,��]( (��z)^k / k! ) = e^(��z)
���̐���n�̊e�ʂ̐��̘a��s(n)�Ƃ���B
f(z) = e^(��z)
>>271 s(x)��9(log[10](x)+1)������
n^5��9(5log[10]n+1)
����n�i�荞��ł��Ƃ͌v�Z�@�B
>>263 ���������܂O�����Ɋg������xyz��Ԃ��l�������
z=f(x,y)�Ƃ��āA�^����ꂽ�͈͂�xy���ʏ�ɂ킽����f(x,y)�𑫂����킹�đ̐ς߂�̂���d�ϕ�
�����̉҂��ĊȒP�Ȗ��ɂ͂��łɉ����ς݂̎��₾�Ƃ��Ă������ł���
�ȒP�Ȗ��͒N�ł��������邩���
>>251 �������ˁB
�ǂ��̒N���Ȃ�ō���́H
n^5 �� 10�i�\���� {log(n^5)/log(10) + 1} ���B >>273 >>272 ���肪�Ƃ��������܂�
�}�N���[�����W�J���̂��̂Ȃ�ł���
>>264 �v�Z���������Ƃ����ƌꕾ�����肻���ł����A�f�J���g���W�n������W�nQ�ւ̎��ԂɈˑ������ϊ�Tx���������Ă���Ƃ��A���x��Q�ɂ�������Wq�Ƃ��̎��Ԕ����̒lq�h�b�g�Ǝ���t�ŕ\�����͉E���̎��ŕ\�������̂Ɍ����邩�A�Ƃ����悤�Ȃ��Ƃ��ؖ��������ł�
�������ςƂ����̂͋�̓I�ɂǂ̂�����ł��傤���H
>>281 �Ō�̂Ƃ���ł���
���ςƂ��Ă���Ȃ��킩��܂��ǁA������Ă��ł����H
>>282 N�~(N+1)�^�s��Tx'(q, t)��N+1������x�N�g��(q�h�b�g, 1)�̍s��ςł�
���h���Ă��݂܂���
>>284 �ex��R^(N+1)�ɂ���
Tx(x+h)=Tx(x)+Tx'(x)h+o(|h|) (h��0)
�����悤��R^(N+1)��M(N, N+1: R)�̎ʑ��ł�
>>279 2�s�ڂ���3�s�ڂ̕ό`���킩��Ȃ���ł����A�ǂ����ċ�̓I�Ȑ����Ɏ����Ă�����̂ł����H
F��W��p��0�̑f�̂Ƃ��鎞
>>287 �Ⴆ��z[k]=x+y^k�Ƃ����đ��قȂ�k l���Ƃ�Ƃ�z[l]��F(x^p, y^p, z[k]) �Ɋ܂܂�Ȃ����Ƃ������Ă����B
��̓I�ɂ́A���������łȂ��Ƃ���Ɛ���P(U,V,W)��W�ɂ��Ă̎�����p������
z[l] = P(x^p, y^p, z[k])
�ƂȂ���̂��Ƃ�邪�W����r�Ŗ����B
�Ƃ���F(x^p, y^p, z[k])�̑S�̂͑S�đ��قȂ�B
�Ƃ��B
�W����r�̂����萸�����ĂȂ�����_�������B
��������S�����B
>>288 ������ƏC���B
�����łȂ��Ƃ����0�łȂ�����P(U, V, W)��Q(U,V)��
z[l] Q(x^p, y^p) = P(x^p, y^p, z[k])
�����݂��Ĉȉ������B
>>275 �i��ł鎖���킴�킴�����Ȃ�
�y���} �����z
���荞�݂����܂���B
>>292 ��������l�����Q�l�Ƃ��R�l�ɍi���čl����Ƃ����ł��B
A, B��2�l�ōl�����
A����肤����t�� 365 �ʂ肠��A���̑��X�ɑ��� B�� A�Ƃ͈قȂ�܂� 364�̑I����������B
����āA365*364 ( = 365P2 ) �ʂ�B
����� 365C2 ( = 365P2 / 2! ) �ōl����Ƃ������́A
�Ⴆ�� {A: 4/1, B: 12/31} �� {A: 12/31, B: 4/1 } �̃p�^�[������ʂ��Ȃ��Ƃ������ł��B
���ɋL�ڂ��Ȃ���A���ʂ͋�ʂ���Ǝv���܂��B
10�̋ʂƂR�̔�������A�ǂ̔��ɂ��K��1�ȏ�̋ʂ�����A�Ƃ����ݒ�̖��Ŏ���ł�
�������F�قȂ锠
{118} : (118) (181) (811)
{127} : (127) (172) (217) (271) (712) (721)
{136} : (136) (163) (316) (361) (613) (631)
{145} : (145) (154) (415) (451) (514) (541)
{226} : (226) (262) (622)
{235} : (235) (253) (325) (352) (523) (532)
{244} : (244) (424) (442)
{334} : (334) (343) (433)
(�Q�l)
http://zakii.la.coocan.jp/enumeration/10_balls_boxes.htm �~C�ɓ��ڂ���l�p�`PQRS�́APQ=a�AQR=b�ARS=c�ASP=d�ł���A�Ίp��PR�̒�����e�AQS�̒�����f �ł���B
���f���̒萔�As�������̒萔�Ƃ���B���f��z�ɂ��Ă̕�����
>>294 ��6�œ����o���Ȃ�
n(a�̔�=b�̔�)=4
n(a�̔�=c�̔�)=4
n(b�̔�=c�̔�)=4
�Ȃ̂�
(36+4+4+4)��6=8
>>297 ���a��abe/��{(a+b+e)(a+b-e)(a-b+e)(-a+b+e)}
�����ŁA���̕����ł��\����B
�Čf���݂܂���B�ǂȂ���������܂��H�H
�����w��2�N�̎҂ł��B���f���_�̖��ł��B
>>301 ����͍���܂����ˁB
�_�����玩�R�ɍl�����q�ׂ������Ȃ����ȁB
�l�Ԃ̔]�̍��{�͏�i�~���{����j�œ����܂��B
�]�ɉ�U�w�I�ȍ��W�@�\�̖�Ɋ��ƍ��W�����܂��B
����Ԃ́A�]�@�\�T���̊��ғI�\���ł���B
����́A�����ē��{�ō��̔\�y�҂ł��鏼�{�����h����^�����\�z�ł��B
�ނ̎��ƂƂ��ɖY����悤�Ƃ��Ă��܂����A�����I�ȏ���w�҂�
�����Nj����Ă��܂��B
���̓��̐��Ɓu����Ƃ�����A�����]�Z���^�[�����肩�ȁv�ɕ����Ă݂�Ƃ����ł��B
�\�[�J���������������̂ɂ܂�����Ȃ��Ƃ��Ă��
>>301 ����Ԃ��\������ނ̈�ЂƂ͍�p�Q�̋O���ł���A�i���`���b�e���w�̌��t�V�т��H
�������ɒނ肾��A�{�C�ɂ��Ă��ꂾ���當�n��w�Ƃ���炩���Ȃ��ق���������B
���ʂ̃I�[�\�h�b�N�X�ȐV�ÓT�h�ߑ�o�ϊw�ł������ʋȐ��Ƃ������̓��l�ފ��菤��ԂŃ~�N���o�ϊw�̋c�_������ǂˁB
�l�Ԃ��܂߂����A���A�������̐����ƔɐB��ڎw�����~����
�u�I�D�v�Ƃ��ċ�ʂ��Ȃ������ʂ��Ƃ����̂���ʂɂ͍������ł��c�_�ł��閳���ʋȐ�������B
�O>>297 C�̔��a��r�Ƃ���ƁA�����藝���A >>207 �O>>310 �lj��A�����B>>300 �������ɂ����Ȃ�B >>300 �w�����̌����Ɏ��Ă��܂����A���o�ߒ��Ŏg���̂ł��傤��
���͂��̖�肪�����܂���ł����B�O�p��Ōv�Z���Ă����̂ŁA�����I�ɂ̓w�����̌����Ɠ����̂��Ƃ�����Ă���͂��Ȃ̂ł���
�G���K���g�ȉɂ������Ȃ��Ȃ�O�ӂ킩���Ă�O�p�`�l���������ǂ�g���Ă��ł���Ȃ��́H
>>302 ���ȉ������܂����A���݂܂���ł���
�����܂���A
�S�������o���ē����W�����������ׂ��̊e���������Ă�����A�S��y-x�ł�����Ċ�����A�̂͂킩��܂����A�����藝�Ƃ̌��т����킩��܂���c
y��萔�Ƃ���fy-fx��x�ɂ��Ă̎����ƌ���
x��萔�Ǝv����g (y) = f (y) - f (x) �Ƃ���
�ׂ荇��(=�@ad-bc=1�����藧��)2����a/b��c/d(�����͑S�Ď��R��)�̊Ԃɂ��镪���̒��ŕ��ꂪ�ŏ��ł���̂�(a+c)/(b+d)�ł��邱�Ƃ��ؖ�����B
>>298 1����2���̃L���������g��E[X]��E[(X-��)^2]�Ɉ�v����̂͂Ȃ��Ȃ̂ł��傤��
x��萔���Ǝv���� f(y) - f(x) �� y-x �Ŋ���B
>>298 z����z�̋��f���ł����H
����Ȃ�Η^���̋����Ȏ�
z��(z��-2����)+����(����z��-z)=sz��
�ɗ^����z��=�̌`�ɕό`�������̂�������Ɨ͋Ƃł����炭�����܂�
>>298 �^������z��/z=�A�����Ȏ�������z/z��=�ɂ���2���������Z���������悩�����ł���
5715
�ӂ�L@Fu_L12345654321
�w�R��1�����������܂����I
�ƂĂ��������ł��I
����������://pbs.twimg.com/media/D-IuUuqVUAALnAB.jpg
����������://twitter.com/Fu_L12345654321/status/1144528199654633477
https://twitter.com/5chan_nel (5ch newer account)
>>312 �w�����̌����Ǝ��Ă���̂́A�]���藝�A�����藝�A
sin^2�{cos^2��1���g���ĐF�X���邩�炩�ȁB
�������w�����̌����݂�����a+b+e��S�Ƃ��ƒu���ĕ\���ƁA
�����ȒP�Ȍ`�ɂ͂ł���ˁB
>>297 �̖��̃|�C���g�́A
���ǁA�ǂ̒������Ɨ����Č��܂��āA
�ǂ����炪�O�ډ~�̔��a�ɉe�����Ȃ������ɂȂ�̂��ɋC�Â����Ƃ��낤�B
�~��ɂ���R�_�����܂��Ă��܂��A�~�͈�ӂɌ��܂�B
����́A�Ⴆ�A��PQR�����܂�Ƃ������ƂƓ������B
���o�p�q�����܂�A���_�r�̏ꏊ�͎��R�Ɍ��߂��Ȃ��B
�܂�A���o�p�q�̊O�ډ~�̉~����̂ǂ����ɂr�����Ȃ��Ƃ����Ȃ��Ȃ�A
�ǂ��Ɏ�����Ƃ��Ă��A�O�ډ~�̔��a�͕s�ςł���B
������A�����́A�i�Ⴆ�A�ja�Ab�Ae�����ŕ\���Ȃ��Ƃ��������Ƃ������ƂɋC�Â��B
���̖��͗v����ɁA�u�~�ɓ��ڂ��遢�`�a�b�̕ӂ̒�����a�Ab�Ac�Ƃ����Ƃ��A
�O�ډ~�̔��a��a�Ab�Ac�ŕ\���B�v
�Ƃ������Ɠ������Ƃ�����悢�ƋC�Â��A�����Ԙb�͊ȒP�ɂȂ�B
�����藝�Ɨ]���藝�i��sin^2�{cos^2��1�j��g�ݍ��킹�āA
�O�ډ~�̔��a��ӂ̒����ŕ\���悢�B
>>323 log( E[exp(tX)] )
= log( 1 + tE[X] + tt/2! E[XX] + ... )
= (tE[X] + tt/2! E[XX]) - 1/2 (tE[X] + tt/2! E[XX])^2 + ...
= tE[X] + tt/2! E[XX] - 1/2 tt (E[X])^2 + ...
= tE[X] + tt/2! E[(X-��)^2] + ...
�� E[(X-��)^2] = E[XX -2X�� + �ʃ�] = E[XX] - 2�ʃ� + �ʃ� = E[XX] - E[X]^2
�p�ꂾ�Ǝv���܂����u�����Ȃ��Q�����v�Ƃ����̂�����܂��B�Ⴆ�A
0 < a[n+1]=na[n]/(n+a[1]+...+a[n]) =a[n]/{ 1+(a[1]+...+a[n])/n } < a[n]
>>315 z=a+ib�ƒu���Ď����Ƌ����ɕ����Ă��ꂼ��A���ł��邱�Ƃ������܂����A����܂��Y��Ȃ����ł͂Ȃ��Ǝv���̂ł����c
���n���ł���Log���g������@���l�����̂ł����A�l�͏�肭�����Ȃ������ł��c
����Ƃ��Ă͍����K���A���_�ŁA�藝�Ƃ��Ă͑Q�����̉���Y�����������̂����E���B���g��ɂȂ邩�ǂ�������
>>332 f(z+h) - f(z) = ��₀¹ dt 1/(t-z-h) - 1/(t-z) = ��₀¹ dt h/{(t-z-h)(t-z)}
L := inf { |z-t| | t �� [0,1] } ( = distance{ z, [0,1] } ) �ƒu��
�C�ӂ̃� (����) �ɑ���, | h| < min( L/2, �� L.L/2 ) �ƂȂ�悤�� h ��I�ׂ�
�E| t-z-h | = |(z-t) +h| �� |z-t| - |h| �� L - L/2 = L/2
�E|f(z+h) - f(z)| �� ��₀¹ dt |h|/|(t-z-h)(t-z)| �� ��₀¹ dt |h|/|(L/2).L| = |h|/|(L/2).L| < ��
����� f(z) �͘A���ł���.
��₀¹ dt 1/(t-z) = log(1 -z) - log(0-z) = log|1 -z| + i arg (1-z) - log|-z| - i arg(-z)
�Ίparg(...) �̑I�ѕ��ɒ��ӂ���Ό㔼�͊ȒP
>>334 �������A����Ã_�@�ʼn�������ł��ˁc�c���肪�Ƃ��������܂��I
�Ȃ�ƂȂ�min{L/2, ��L.L/2}���l����Ƃ��낪�A�����̏��̘A�����̏ؖ��Ɏ��Ă�C�����܂��c�c
�@��z'/z = z -2�� + ���� -s,
>>321 �t�@���C����Ŏb���F��ȃT�C�g������ł����Ǎs�Ƃ��g���Ă��Ă悭�����ł��Ȃ��ł�
�^����ꂽ������ό`�Ȃǂŏؖ��͂ł��Ȃ��̂ł��傤���H
>>337 ��w�ւ̐��w�̑����̐V���w���K�ɍڂ��Ă��͂�
>>337 ���ʂ����ǂ��Ă��Ώؖ��͗����ł��邾�낤���ǁA����ŏI���ł̓_������H
�L�`����(a,b), (c,d)�ƌ��_��3���_�Ɋ܂ޕ��s�l�ӌ`�̎��A�����Ɋi�q�_��4�����Ȃ����ƁA���ꂪ�ǂ̂悤�Ɏ咣�ɂȂ����Ă������������Ȃ��ƁB
�s��͐��w������Ȃ�K�{�Ȃ�������Ƃ���B
>>339 �m���ɂ��������Ǝv���܂��B
�������܂����Z���Ȃ̂ō��̒m���Ǝ��͂ŗ����ł����@�ł͉����Ȃ��̂��ȁA�Ǝv���Ď��₵������ł��B
���s�l�ӌ`�𗘗p������@�ł͎����ł͋��炭�������肳�ꂽ�����ʼn����Ȃ��Ȃ肻���Ȃ̂Ŏ��ό`�Ȃǂ����������@��T���Ă��܂��B
�Ԃɂ��镪���� p/q �Ƃ���
f(x,y)=|xy|���Δ����\�ȓ_���Ăǂ����߂�����ł����H
�k�ޑ�l
������
>>341 c/d<p/q<a/b�Ƃ���(�A��ad-bc=1)
p/q-c/d=(dp-cq)/dq>0
a/b-p/q=(aq-bp)/bq>0
dp-cq=s,aq-bp=t�Ƃ���
2����A�����ĉ�����
q=bs+dt
�������
p=as+ct
�����
p/q=(as+ct)/(bs+dt)
�e���͎��R���Ȃ̂Ŗ��炩��s=t=1�ōŏ��ł��肻�̂Ƃ�
p/q=(a+c)/(b+d)
�����Ă܂���?
>>346 p/q=(a+c)/(b+d) �̕��q����̍ő����g�Ƃ�����
�݂��ɑf�Ȏ��R��mn��p����
a+c=gm,b+d=gn�Ƃ�����
���̂Ƃ�p/q=m/n�ƂȂ�p=m,q=n
b+d���ŏ��ƂȂ邩��n=b+d�ł���Ag=1
���������Ċ���
>>347 p=a+c, q=b+d �̂Ƃ�������ؖ����Ă��_���Ȃ̂ł́H
p/q �͂���ȊO��c/d��a/b�̊Ԃ̌��Ȃ���B
�܂�p=as+ct��q=bs+dt��GCD��1������Ȃ��ƁB
��ʂɂ�ad-bc=1����s��[[a,b],[c,d]]�̒�߂�ꎟ�ϊ���Z�W���ʼnt�Ȃ̂𗘗p����
gcd(p,q)=gcd(1,1)=1
�Ƃ��������Ǎs��g�������Ȃ��Ƃ��ґ�Ȃ��ƌ����Ă邩��ȁB
�������s��g���Έꔭ�ōςގ����O�`���O�`�������I�ȕό`�����ł������邾�낤���ǁA����Ȏ����ĂȂ�̖��ɗ����̂��B
>>330 >>1 �ł� �����Ă͍���Ƃ������Ƃł����p�I�ȋ@�\��lj����Ă�����
https://pastebin.com/hzdfNr6t ���������Ȃ�O��Ƃ�������
1�̈����ŁA���ꂪ�f��������B�f���Ȃ炻���Ԃ��B�{���Ȃ�Ԃ��Ȃ��B
2�̈����ŁA����2�̋�Ԃ̑f�������������B1���ȉ������K�v�ł��R�[�h�Ɏ������K�v�͂Ȃ��B
���̏���� ��̏��jpg�摜�����肪���E��
���Ȃ݂Ɉ��������ł�txt �o�͂�5GB�ŁA7zip�����500MB���x�Ɏ��܂�
>>352 ���� PARI/GP ���Đ����\�t�g��d�����Ɏg���Ă�B����I�X�X������B
���Ȃ�y�ʂ������_�W�̃R�}���h���[�����Ă�B
������Ƃ����v���O�����������邩�炻�������~���ɂ������Ă����Ǝv���B
>>353 thanks
GPL �̃}���`�v���b�g�t�H�[�����ꂩ
�l�I�ɂ͓d��Ȃ� Common Lisp ���C�ɂ����Ă���
---
���傹��f���W�F�l���[�^�͂��݂₰��
�̂̎����͑傫�ȑf���������Ă���f���\���M�d���Ǝv���Ĕ��������Ƃ�����
���������ꂪ����L�����̂悤�ȂԌ����f���\���o�ł��ꂽ�Ƃ��Ă��A
�����K�v���Ȃ�
�����Ȃ��݂₰�Ȃ�
PARI/GP �A�Ⴆ��...
>>355 ���̑傫�Ȑ��Ŏ��p�I���Ƃ����
�v�Z�ς݂̑f���L�^���ăL���b�V���ɂ��Ă邩����
(�f���藝�ɂ��Ɩ�230�{�̑��x�Ōv�Z���Ă���͂�)
����������͐S�z�����ǁA���ɕ֗�����
��[k=0,n] {C(n,k)}^m ���Ă����a���킩��܂���B
�D�����藝�g��������ł�����|n*sin(x/n)*{x*(x+1)}^(-1)|���ォ��}������̗���ĉ�������܂���
>>357 >>351 (����)
n
>>1 �ł�
�@a[n]�@�`�@37.9/n^s,
�@a[1] + a[2] + ���� + a[n]�@�`�@s - 16.1/n^(s-1),
�Y�����Z�ɂ��Ăł��Bv��3�����x�N�g��
>>363 �E(��_ijk)(��_ij�fk�f) = ��_jj�f��_kk�f - ��_jk�f��_kj�f
�����̌������o���Ă�����
�x�N�g����͂̌����Ŗʓ|�Ȃ�̑唼����u�œ��o�ł���悤�ɂȂ�܂��B
(���͂Łu�����v�������͂ǂ����ċ����Ă���Ȃ������I�Ǝv���܂���)
|w|^2 = (w_i)(w_i)=(��_ijk)(��_ij�fk�f)(��v_k/��x_j)(��v_k�f/��x_j�f)
= (��_jj�f��_kk�f - ��_jk�f��_kj�f)(��v_k/��x_j)(��v_k�f/��x_j�f)
= (��v_k/��x_j)(��v_k/��x_j) - (��v_k/��x_j)(��v_j/��x_k)
= tr( M(M^t - M ) )�@(�s��: M_ij = ��v_j/��x_i �ƒu���܂���)
�Ō�̕ό`�͕K�v�Ȃ̂�������Ȃ����ǓY���������������Ȃ炱��Ȋ����Ƃ������ł�
>>356 100�����炢�Ȃ�����̑f������@�ŏ\���ȑ��x�͏o���Ȃ��̂���
>>359 �����܂���|n*sin(x/n)*{x*(x+1)}^(-1)|����Ȃ���|n*sin(x/n)*{x*(1+x^2)}^(-1)|�ł���
>>365 ���ׂ���isprime����1000���̔����15���`30��������A�Ə����Ă������̂��������B
WolframAlpha�搶�Ɏ�����isprime 10^1000+453�����炷���ɑf���ƕԂ��Ă������ǁA����͂ǂ�����Ĕ��肵�Ă�̂��˂��B
>>367 ���łɌv�Z�ς݂̃L���b�V���w�������ł���
��̕��� PARI/GP �𐄂��܂������A���� python�ʼn��ł��ł��܂��ˁB ������������Ȃ�ł��ˁB
�Ⴆ�� PARI/GP �̏ꍇ
>>369 ����Python�͂��܂�ɑ������邯�ǂ���ς�L���b�V���Ȃ̂��ȁH
|length: 2 {10^1000+0...10^1000+1999 �͈̔͂ɑf����2����}
�����ЂƂ�10^1000+1357
�����WolframAlpha�͑����ɔ��肷��
>>371 wolframengine �C���X�g�[�����Ă���Ă݂���
�ُ�ȑ�������
�I�t���C���ɂ��Ă��ς�Ȃ�����I�̃f�[�^�x�[�X�ɖ₢���킹�Ă���Ȃ�
2����sqrt prime �܂ł̑f���Ŏ����Ɋ����Ă���
�悤�ȑ��x����Ȃ�
��͂�n�b�V���A�f�����L�[�Ƃ��Ă��ꂪ�f�����ۂ����v�Z�ς݂̃n�b�V����
���ׂĂ���悤�ȑ��x��
�t�@�C�����̂��߂ɑ傫��n�i�����g���Ă���̂��A�Ǝ��o�C�i�����g���Ă���̂�
�ڐ��͂��Ȃ��������������Ƃ��Ǝv�� ��������
>>371 ���ǁA���̓���f���Ȃ�ł��ˁB�f������Ȃ����̔���͈�u�ŁB
��͂荪�{�I�ȃA���S���Y�����Ⴄ�̂ł��傤
> ���܂�ɑ�������
�~���b�\���� t*(10**3) �Ƃ���ׂ��ӏ��� t*(10*3) (= t*30 ��...) �ɂȂ��Ă܂����B
import time
import gmpy2 as gm
t=time.time(); li= list( filter( lambda n: gm.is_prime(n), [10**1000+k for k in range(2000)])); t=time.time()-t
print(f" length: {len(li)}\n time: {t*(10**3):7.2f} msec\n" )
--->
length: 2
time: 3529.49 msec {����ł�����}
import time
import sympy.ntheory.primetest as sm # gmpy2 ���� sympy�p�b�P�[�W�̕����L�� (���Ԃ�)
t=time.time(); li= list( filter( lambda n: sm.isprime(n), [10**1000+k for k in range(2000)])); t=time.time()-t
print(f" length: {len(li)}\n time: {t*(10**3):7.2f} msec\n" )
--->
length: 2
time: 5270.99 msec {������Ƃ����x���B�A���S���Y�����قȂ�̂������Ȏ����e�N�j�b�N�̍��Ȃ̂��͕s��}
>>373 �f������Ȃ��� �{������
�Ƃ�������Ȃ�
6k +-1 �̌`�����Ă��Ȃ� �Ƃ�
������x�傫�����A1���ڂ�1,3,7,9�ł͖����Ƃ�
�̔��荬����Α����ł���
�����傫���Ƒf������Ȃ��ق����傫���̂ŁA
�������������ɔ{�����艺������@����ق���
�������o����͂�
PARI/GP �͐��_�W�̃\�t�g�E�F�A�Ƃ��Ă͘V�܂Ȃ̂ŁA���������̂���ĂȂ��͂����Ȃ��Ǝv����ł����ǂ˂��B
�Q�_�̖��ł������肢���܂�
>>363 ���肪�Ƃ��������܂��B�C�v�V�����̊W���A�悭�o���Ă����܂��B
wolfram engine ��
https://www.wolfram.com/technologies/nb/index.ja.html?footer=lang >�m�[�g�u�b�N���e�L�X�g�G�f�B�^���ŕҏW����ƁC�����ȃL���b�V���f�[�^���g����\��������܂��D�����h�����߂ɂ́CWolfram����x�[�X�̐��i�ȊO�Ńm�[�g�u�b�N��ҏW����ۂɁC�t�@�C���㕔�t�߂ɂ���CacheID���w�肵���s��K���폜���Ă�������
�ȂL���b�V���̐���������ˁB�����I��
>>376 ���~�X�ł���
�~ (G:H)=k
�Z |G/H|=k
10�i�@�\�L���ꂽ���R��k�̊e���̐��𑫂����킹���l��f(k)�Ƃ����B
>>383 �i1�j��1,2,3,4,5,6,7,8,9�ŁA����ȏ��n=a[i]*10^i+...�ƕ\�L����Ηe�Ղ�n>f(n)�ł����B
�i2�j��log10���u����-1�v�Ȃ̂�111...110�̂悤�ȏꍇ�ɃC�R�[���ɂȂ邱�Ƃ͕�����܂����B���̐�̏ꍇ�������悭�킩��܂���B
>>376 ��������̂���ˁH
G���ʐ�10�̓�ʑ̌Q�AH���V���[2�Q�Ƃ����k=[G:H]=5��|G|=10��5!=120�Ŋ����Ȃ�����H�̕����Q��G�̐��K�����Q�ɂȂ�͎̂����Q�����Ȃ����ǁH
>>382 �m�I��Q�҂͂₭�a�@�s��
>>385 ������ۂ��ł��ˁc�c
�ʂ��ԈႦ�ĂȂ��̂Ŗ�莩�̂��Ԉ���Ă��̂���
>>359 >>366 | n�sin(x/n) �x^(-1) | < 1�@���g�����炢�������ˁH
>>392 (1) f(��) = cos4�� - {�P��������} ������ő�l�͒���������B
�������ċɒl���Ƃ�_��T���ŏ��l��������B
(2) f(x) = x^3 -3x �� y=x �̃O���t��`���Ε�����B
>>393 �����Ɠ�����������̂����Ƀq���g�݂����Ȃ̏o���ď������C�ɂȂ��Ă邨�܂��݂����ȃS�~����Ԏז�
2��ڂ͓���̉ߋ�����ȒP�ɂ����o�[�W�������ȁB
1��ڂ͔�������K�v����Ȃ��B
2��ڂ͂��Ƃ�2004�N���嗝�Ȃ̑�S�₾�ȁB
�w�i�ɂ���`�F�r�V�F�t�̑��������������Έꔭ�����A�}�l������I�Ɏv�����ē��_�ł����@�ł͂Ȃ��B
���ꂨ�肢���܂�
>>394 �ւ��q���g�����ƈ̂����ȂA�N�ς���Ă�ˁB
>>394 �����̖{���ɖ��ɗ����Ȃ����ƌ����Ă�S�~
���������ז�����
>>394 �����Ă��������A�z��id�ւ��Ƃ�����Ə������ނ��
�������N�Y�Ȃ̎��o���Ăق������A�N�Y������킩��Ȃ�
���������炱�̎�̃L�`�K�C�ɂ͑Ώ��ł��Ȃ��̂��h����
>>392 >>396 >>392 >>398 ���݂܂���s��̊�{�I�Ȃ��ƂŎ���Ȃ�ł�����2�~1�s��~2�~2�s����Čv�Z�ł��܂����ˁH
���w�̊F�l�A�����悯��Ή��������肢���܂�
�~����=2�𐔊w�I�Ɍ����ɏؖ������������������������������L���E�F�G�G�G�G��������
http://2chb.net/r/news4vip/1563916696/ ���̖�肪������܂���B
>>407 ���W��2����������2���Ȃ̂� �� = r*e^{+i��}, �� = r*e^{-i��} �ƒu��.
�Er = |��| = |��| = 1 �ł���.
�����łȂ��� n���� �� ���U�܂��� 0 �Ɏ�������.
2 cos(n��) = e^{+in��}+ e^{-in��} = e^{+i(n+p)��}+ e^{-i(n+p)��} = 2 cos((n+p)��) �ł���,
����� cos(n��)=cos(��) �ƂȂ�̂� �� = n�� + 2�� N �܂��� �� = -n�� + 2�� N (N�͐���)
�̏ꍇ�Ɍ�����. �܂� p�� = 2�� N �܂��� (2n+p)�� = 2�� N
������ɂ���
�E�� = �� Q (Q: �L����) �̌`�ɂȂ��Ă���.
�t�ɂ��̂Ƃ��������������͖��炩.
���ƌW���̊W���
a = -(��+��) = - e^{+i��Q} - e^{-i��Q} = 2 cos(��Q)
b = ���� = e^{+i��Q} e^{-i��Q} = 1
( ����� ��=��=0 �̓i�V�Ƃ����Ă��������
�ꉞ�� x^2 = 0 ��2�d���ł���. �����P�Ƃ��ĉ��Ɋ܂߂���������R�� )
>>407 ����Ȃ�����ɂ���Ȃ��ĂȂ��B
����������
a=-2cos(2��/p)�ƂȂ鎩�R��p�����݂��Ab=1
�Ƃ����낤���ǕK�v�\�������Ȃ�ӂɒ�܂���̂ł͂Ȃ��B
�ǂ��̃J�X���������肩�m��ǂ�Ȏ����������z�̍�������Ȃق��Ƃ��B
(3)�̉������Ē��������ł��B
�܂��A(2)�ɂ��āA
B�����Ȃ�Bx=0��������x�����݂���̂ŏ����ɔ��������B�����B�͐����B
�Ƃ����c�_�ʼn������̂ł������ꂾ�ƁqBx,x�r�������Ƃ�������������܂���B�Ȃɂ��Ԉ���Ă���̂ł��傤���H
�ǂȂ�����낵�����肢���܂��B
�ȉ��̏ꍇ�����ؖ��@�͂ǂ������Ӗ��ł����H
>>408 ��=0 �̂Ƃ��A���܂��̓�^p-1�̂����ꂩ��0�łȂ���Ȃ�Ȃ��B��=0�̏ꍇ�����l�B
����Ă��̂Ƃ���(a,b)�̎������́A(0,0),(1,0),(-1,0),
>>405 �N���l�b�J�[�ςȂ���Ȃ�
>>410 (2)�Ɋւ��Ă͗]�v�ȏ�����������܂��A
�G���~�[�g�s��̘b�Ɍ��肵�������������ł��傤�B�Ԉ���Ă͂��܂���B
(3)
C,D ���X�G���~�[�g�s��Ȃ̂ŁA�ŗL�l(n��, ����)�A�ŗL�x�N�g��( n��) �����̂悤�ɂƂ鎖���ł���.
s=rank(C), t=rank(D)
ci��0 (i=1..s), �@ci=0 (i=s+1..n)
di��0 (i=1..t), �@di��0 (i=t+1..n)
C.Vci = ci.Vci, �@D.Vdi = di.Vdi (i=1..n)
��Vci, Vcj�� = ��Vdi, Vdj���@= ��[ij]
�ϊ��s��: P (����) ,�@Vci = P[ij] Vdj
�������
�E��D.Vdi, Vdi�� = di �� 0 (i=1..n)
�Ei=s+1..n �̂Ƃ��A0 = ci = ��C.Vci, Vci�� �� ��D.Vci, Vci��
�@= ��{jk} P[ij]P[ik]^* ��D.Vdj, Vdk�� = ��{j} P[ij]P[ij]^* dj �� 0
����� P[ij] = 0 (i=s+1..n, j=1..t) ---(A)
�s�� P���x�N�g���̕��� (p1,...,pn) �Ƃ݂Ȃ��ƁA
���� p1..pt �� �ꎟ�Ɨ��ł���A(A)�ɂ������I�ɂ� s�������x�N�g���ł���
����� s �� t (���x�N�g���̈ꎟ�Ɨ���)
>>414 �������킩��Ȃ��_������̂ł���
1
Vci = P[ij] Vdj
�Ƃ�����̂͂Ȃ��ł��傤���HC�̌ŗL�x�N�g����D�̌ŗL�x�N�g���̒萔�{�ɂȂ�̂ł����H
2
(A)��j�̏�����j=1,�c,t�ƂȂ��Ă��܂���j=1,�c,n�̊ԈႢ�ł����H
���� ^*�͕��f�����ł���ˁH
���2��������Ό�͗����ł����Ǝv���܂�
��낵�����肢���܂�
��`���{k��ℤ|0��k��n},n��ℕ��萔�Ƃ���
>>415 1. Vci = P[ij] Vdj = ��{j=1..n} P[ij] Vdj �ł��B
�����Y������2�o�Ă�����a���Ƃ�u�k��L�@�v�̂���ł����B
����ŁA ... = ��C.Vci, Vci�� = ... ���̓Y������ i ���Q�Ȃ̂� �a���Ƃ�܂���B
�L�@�̓��ꂪ�ł��Ȃ����͂��܂�g���ׂ��ł͂���܂���ˁB
2. j=1,�c,t �́A���̂܂܂ł��B
dj �� 0 ���������Ă���̂ŁA0 �� dj �� 0 ( j = 1.. t ),�@dj =0 ( j = t+1..n )�@
����āA
0 = ci = ��{j=1..n} P[ij]P[ij]^* dj
= |P[i1]|^2 d1 +|P[i2]|^2 d2 + ... + |P[it]|^2 dt + 0 + ... + 0 = 0
�� |P[ij]|^2 dj = 0 (i=s+1..n, j = 1.. t )
�� P[ij] = 0 (i=s+1..n, j=1.. t)
3. �u^*�͕��f�����v�ł�
�����I�ɂقږ��炩���Ǝv���̂ł����A�L�q���ǂ������炢����������܂���B
���_��ے肷��Ɓ�APB�A��BPC�A��CPA �̂���90���������ӂ��B
>>417 ���J�ȉ���{���ɂ��肪�Ƃ��������܂�m(_ _)m
���������ł��܂����I
>>416 f(k) = ��[j=0,k-1] n�bj = 2^n - n�bk 2�e1(1, -(n-k); k+1)(-1),
�������@n�bk = n!/{k!(n-k)!}�A2�e1(a,b;c)(z) �͒������B
y��x�Ŕ������邱�Ƃ�dy/dx�Ə����A����͕������ł͂Ȃ������ۂ̌v�Z�ł͕����ł��邩�̂悤��dy��dx��藣���Ĉڍ�������ł��闝�R��m�肽���ł��B
>>422 ��w���̖��Ƃ��Ă͂��Ȃ�ȒP
��/10=18��
2��/5=72��
������90���Ȃ̂Ł�(1-tt)
cos5��
=cos(3��+2��)
=cos3��cos2��-sin3��sin2��
=(4cos^3 ��-3cos��)(2cos^2 ��-1)-(3sin��-4sin^3 ��)(2sin��cos��)
=(4cos^3 ��-3cos^2 ��)(2cos^2 ��-1)-(3-4sin^2 ��)(2cos��)(1-cos^2 ��)
�����cos��=z�Ƃ���
cos5��
=(4zzz-3z)(2zz-1)-(1-zz)(2z)(4zz-1)
=16zzzzz - 20zzz +5z
cos18��=��(1-tt)=k�ɏ��K�p�����cos90��=�[���ɂȂ�̂�k��0�Ƃ��킹
16kkkk-20kk+5=0
k^2=1-tt��������
16tttt-12tt+1=0
t=cos72��<1/2=cos60��
�����1/4>tt=T>0�Ƃ���
16TT-12T+1=0
������T=(3-��5)/8
���̍���������t=(��5-1)/4
���Ȃ�ȒP���ˁB�k��ł��o����
>>423 ���̒�{��͊T�_��P37����2�y�[�W���炢�ǂ�
��ӏ��������������Ă��B�����͕ς����܂��
>>422 ���Đ_�ˑ�ł����N���O�ɗޑ肪�o�ĂȂ����������H
�`���[�g�ɂ��ڂ��Ă����ȋC������i���m�F�j
d/dx(f)��d/dx�́Af��x�Ŕ��������p�Ƃ����Ӗ��ŁA�����Ƃ͈Ⴄ�̂ł͂Ȃ���Ă���
�����ǂ�����ɉ����ē��Ă͂߂čs�������̂��ɂЂ˂肪�S���Ȃ����v�Z���n�[�h����Ȃ��̂�
�ؖ��@n���f���łȂ��Ɖ��肷���
�v���o����
>>422 ��=1/5�Ƃ����āA3��=��-�Q�Ƃ��g���̂��y�����ǁAcos(5��)�����߂�Ƃ������邵�c
���������A���n�̖�肾����
(cos��+i sin��)^n = cosn�� + i sin n�� ���g���Ă�����Ȃ��́H
���ꂼ��萔�łȂ�3�̎����W���̗L����A,B,C�ɑ�
��̓I�ɂ͎��̖����l���Ă��Ă̋^��ł��B
�_�������ǂ��Ȃ��Ă�̂��悭�킩���
lim[n����] (1+1/n)^n (e�̒�`��)
lim[n to inf] cos(2��en!)
>>440 �����A�ʔ����B
�ؖ��ǂ�Ŕ[�����邵���Ȃ��Ȃ��B
�吔�ɂ͏ؖ��ڂ��ĂȂ��̂��ȁH
exp(1)���}�N���[�����W�J����n!e�̒[�������R�[�V�[��ɂȂ�ˁB
�ʔ����B
�Ȃ܂�܂��̘b�荡�N�ɓ����Ă��炱�̃X�����ʔ������X���Ō����C���������
n!�łȂ��Ƃ��A�w������葬�����U������ɑ��Ă͈�ʂɂ������������\���ł���Ƃ������_�ɂȂ��Ă��C������
e�ɂ��邩�番����Â炢���
en!������ƑS����������
x^2+y^2=y��}�ɂ���Ƃǂ�Ȑ}�ɂȂ�܂����H
�ؖ��@n���f���łȂ��Ɖ��肷���
��������n���f���Ȃ�An��ab�ɋ�̓I�Ȑ��l�����čl���Ă݂邱�Ƃ��s�\�B
�}���z�[�����Ȃ��ۂ������~�͒蕝�}�`�Ȃ̂ŁA�ӂ�������Ă����̒��ɗ����Ȃ��B
���w�I�ɂ͉s�\
>>439 http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q128032107 >>450 �Ȃ����w�I�ȉ��߂�����Ƃ��ɏo�����肪�������Ƃɂ���̂����킩��Ȃ�
�}���z�[���̖��͐��w�I�ɂ�
> ���a48cm�̊ۂ����ɁA���a50cm�̊ۂ��t�^��ʂ��邩
�Ƃ�����肾�낤
�u�~�ł͂Ȃ��Ⴆ�Ύl�p�`�̏ꍇ�͏o�����蕔�������̂������L���Ƃ�Ȃ���Ȃ�Ȃ��Ȃ邩��v�������Ƃ��Đ������̂����m��Ȃ�����
�u�l���ʂ邱�Ƃ��\�ł���A���A�W�������邱�Ƃ������悤�ɂ��A���A�ޗ���ł������Ȃ�͉̂~������v�������Ɛ������̂����m��Ȃ�
>>453 �L�`�K�C�Ƀ}�W���X����Ȏז�
���R�r�A���Ɩʑf�x�N�g���̕����̌��ߕ��Ɋւ��Ď���ł�
�ؖ��@n���f���łȂ��Ɖ��肷���
>>455 �����łǂ���`���邩����
r, �� �� x, y ���ɍ��W�ɂ��� mapping ��������������
(��/�݃�)�~(��/��r) �� -z �����ŁA��ɊJ���������ʂȂ�O�����Ƃ�������
>>457 >>457 ���ʂ̍��W�ϊ����x���Ȃ��3�������������ȕω��̕����͌��Ď��邩�炻������O�ς̕��������銴������ʓI�ł����ˁH
>>445 ������₷��
�����I�ȗ����ł����Ȃ琮�������������ł���Ƃ��낪�~�\���Ă��Ƃ���
>>445 �ƂĂ�������₷���������Ă��������Ă��肪�Ƃ��������܂��B
���������������ł���Ƃ����̂́A���o�I�ɂ��[���ł��܂����B
10^m���ƈ�ڗđR�ł��ˁB
>>462 �킴�킴�����قǂ̂��Ƃł͂Ȃ�����
�ꉞe*n!�̏����������[���Ɏ�������ؖ��������Ă�����
e=��(k=0����) 1/n!������
n!�{�����k=0-n�̍��͑S�������ɂȂ�
���̍������ɏ�����1/(n+1),1/(n+1)(n+2),1/(n+1)(n+2)(n+3)�c��
��=1/(n+1)�Ƃ��āA���ꂼ�ꃿ�A��²�A��³�c�c�Ɠ��������������Ȃ̂ŁA
���̗ݏ�̖����a�ŏォ��}���āA�����̘a��1/n��菬����
������n�����Ń[���Ɏ�������
�ؖ��@n���f���łȂ��Ɖ��肷���
�ؖ��@n���f���łȂ��Ɖ��肷���
�܂��A�����ؖ��������̂������Ȃ����B
>>448 �E�̉摜�̂悤�Ɍ��܂������a�̉~�����Ԃ��Ȃ��悤�ɏd�˂Ă������ꍇ�Ȃ�ł���
�d�Ȃ��������̗v�ʐς�
�~�̒��a���Ⴆ�� 5cm��10cm�ł͂ǂ��炪�傫���Ȃ��Ă�����ł��傤���B
�d�˂闦�ɂ����Ǝv���܂����X�������ł��킩��Ə�����܂��B
>>469 5cm�̏d�Ȃ�̐}�S�̂��{�����炻�̂܂�10cm�̐}�ɂȂ�
���̂Ƃ��d�Ȃ�̖ʐς�4�{�ɂȂ�d�Ȃ�̌���1/4�ɂȂ�
���������đS������
>>470 ���肪�Ƃ��������܂��B
�ƂĂ��킩��₷�������ŗ����ł��܂����B
���̂܂܂Q�{�ϊ������Ɣ��z����悩������ł��ˁB
������܂����I
>>450 ���w�I�ɉ��߂����
���̗��R�Ȃ�A�蕝�}�`�ł�������n�Y��
�ۂł���K�v�͖������Č��_�ɂ����Ȃ��
�Z�b�N�X�������̂ł������肪���܂���
(�x�X�g�A���T�[)
>>466 >>467 >>476 >>478 �킸��4�����炸�ł��̃��X��������B
�������^�C�s���O�͂ł��ˁB
�����܂���B�C�Â��܂����B
___����___�f���ɔ����� >>469 �~���l�߂��~�̔��a��r�Ƃ���ƁA�~1��������̏d�Ȃ蕔���̖ʐς̔����́A >>311 �A���A�P�ʖʐς�����̏d�Ȃ蕔���̖ʐς́A �O
>>481 �P�ʖʐς�����̏d�Ȃ蕔���̖ʐς́A
(1-3��3/2��)�~100��17.3(��)
������u�P�ʖʐς�����̏d�Ȃ蕔���̖ʐρv�ƌĂ�ŗǂ����̂��A�͂Ă���
>>477 �K�v�Ȏ���������
�]�v�Ȏ����菑������
�Ӗ��s���ȏؖ��ɂȂ��Ă��܂�
�܂��A�����ϐ��̒�`�͑S�ď���
a,b�͉����H
n���������ł���Ɖ��肷���
���鎩�R�� a,b �����݂�
n = ab (1 < a �� b < n)
�����B
1�X�e�b�v���Ƃɕ��͏���
> n�́�n�ȉ���a�̖̑f���Ŋ�����
�ł͂Ȃ��A
a > 1 �ł��邩��Aa��f������������� 2�ȏ� a�ȉ��̑f������1�͂���B
����� p �Ƃ���A p �� a �� ��n �ł���B
p�� n = ab �������B
�u����̏����v�Ȃ�ĉ��������ɁA�������ׂ��B
��蕶��ؖ����ɂ́AA��B�Ƃ����`����������A
�ǂ̉��� A ���w���Ă���̂��s���ĂɂȂ�₷���B
���������āA
���R�� n �������� �� n �������f�� p �Ł�n �ȉ��ƂȂ���̂����Ȃ��Ƃ� 1�͑��݂���B
���������B
�������
���R�� n �� ��n �ȉ��́A�ǂ̑f���ł������Ȃ����
n �͑f���ł���B
����A���l65�i���l70�͖��̂܂����j����
��`�����l���W�Ȃ��B�ؖ��Ȃ��Ȃ��Ă����B�O>>482 �킩��Ȃ�����������B�Ƃɂ����k�o�����ē������o���B���ꂪ���w������[�����B >>478 �������ݍӂ���
�@����P : �u n����n�ȉ��̂ǂ̑f���ł������Ȃ��v(p) �Ȃ�� �u n�͑f���ł���v(q) (�_����: p��q)
���ؖ�����Ƃ������ł��B
�E�ؖ�A
P �̑�� �u n�͑f���łȂ��v�Ȃ�� �u n����n�ȉ��̂���f���Ŋ�����v (��q����p)
(... ���� ...) �ؖ��ł����̂ŁAP �͐^�ł���B
�E�ؖ�B (����������⌵����)
�u n����n�ȉ��̂ǂ̑f���ł������Ȃ��v(p) �Ɓu n�͑f���łȂ��v(��q) �����ɐ^�ƂȂ鎖�����蓾��Ɖ���
�܂� ��n ( p�ȁ�q ) ���^�ł���Ɖ���
(... ���� ...)
�u n����n�ȉ��̂���f���Ŋ�����v(��p) �������ꂽ������ł��� p �Ɂw�����Ă���x���߁A����͖����ł���B(�� �r����)
�܂� �ʁ�n ( p�ȁ�q ) ���^�ł���Ƃ̌��_
����� p �Ȃ�� q �ł���B(�� �ʁ�n ( p�ȁ�q ) ) = ��n ((��p)��q ) = ��n ( p �� q ) )
�ꉞ�A�p������Ă����ƁA�_���� : p��q = (��p)��q �ɑ���
�@�ے�: ��(p��q) = p��(��q)
�@�t: p��q = p��(��q)
�@��: (��p) �� (��q) = p��(��q)
�@��: (��p) �� (��q) = (��p)��(�ʁ�q) = (��p)��q (�܂� p �� q �Ɠ��l)
�ƂȂ��Ă��܂��B
�u�ے�(��...�ɔ�����, ...�̔���)�v�Ɓu�t�v�͈قȂ�T�O�Ȃ̂Œ��ӂ��K�v�ł��B
>>480 ���̕ӂ肪�܂��S�b�`���ɂȂ��Ă�悤�ȋC�����邯�Ǒ��v�H
���̂Q�̕\���͑S������Č����܂����A�ʕ����ēW�J����Ɠ������l����邱�Ƃ��킩��܂�
����͉��̂Ȃ̂ł��傤���H
�ǂ�������猩�����܂����H
a�Ŋ���ƁA
Excel�̃Z����[=NORMINV�iRAND(),10,1�j]�Ɠ��͂���ƕ���10�W����1�̐��K�������\�������̂ł����A
>>487 >>489 ���̎����������������
VIDEO ����ɂ��Ă��@�����̍D���Ȑl���ȁB�B�B
>>492 �s�Ε��U (n/(n-1))s^2 �̊��Ғl�� ��^2 �ł��B
>>496 ���肪�Ƃ��������܂��B
���v�w�I�ɐ����ł������Ȍ��ۂ炵���Ƃ������Ƃ�������܂����B
�������Ȃ���A���͐́A���v���菀�ꋉ�͍��i���܂������A���������̂͗\�z�ł��܂���ł����B
�����������Ƃ𐔊w�I�ɗ����ł���悤�ɂȂ�ɂ́A����ς莄�̕�������܂���ˁB
�ꋉ���i��ڎw�����C���o�Ă��܂����B
https://imgur.com/SFxFvYQ ���̖������䋉���H�̖��̉��������������������Ⴂ�܂����H
�������̃A�v���[�`�����ł������Ăق����ł��B�B�B
>>498 ���O�����W���̖���搔�@�ʼn�����Ǝv���܂���
n�捪��^(1/n)�ő�p���邱�Ƃɂ��܂�
��((x-exp(2��ki/n)2^(1/n))^m-3)
>>501 ������č��Z���x���܂ł̐��w�Ŏ������Ƃ��ĉ\�ł����H
���l�̂Ƃ����̂͌Q�̂̑̂ł����H
>>501 ����ĂȂ����ǁAn��m�ɊȒP�Ȑ�������ėl�q���ώ@���Ă݂ẮH
>>504 �N�ł��ł������Ȃ̂́A�D�L�����Ƃ���ƈڍ����J��Ԃ��ċA�[�@
�Œ�����Ƃ߂�ǂ�������
>>499 >>500 >>503 ���O�����W���E�E�E���O�����͕��������Ƃ���܂��B�B�B
�����܂��I���肪�Ƃ��������܂��[�I
��ʓI�ɍׂ������Ƃ͖�������z=f(x,y)�ŕ\�����2�ϐ������������Ƃ�z=c�̕��ʂ�\����������f(x,y)-c=0�ł���ˁH
>>446 ���S��(0,1/2)�̔��a��1/2�̉~
>>498 ���O�����W���ł�������
���������n��2�̏ꍇ�Ŏ����Ă݂�Η\�z�����悤�ȃV���v���Ȃ��̂�����\�z���Ă�������������ł��悢
�������獂1���x���̐��w�ʼn���������������
����_�ōő�ɂȂ�Ƃ��āA�Ⴆ��x1��x2���قȂ��Ă�����
���炵�Ăǂ��Ȃ邩�Ƃ���
�v�͑S���ϓ�����Ȃ��Ⴟ����Ƃ��炷�����ł����Ƒ傫��S��������ĊȒP�Ɏ�����
>>498 >>501 >>506 �����̌W���́@(x^n - 2)^m + (x^m - 3)^n - x^(mn)�@�Ɏ��Ă邯�ǁA�Ⴄ���....orz
>>498 >>505 �������B
�Ǐ��I�ɂ̓��[�N���b�h��Ԃƌ��Ȃ���悤�ȁA�}�`���ԁi�ʑ���ԁj�̂��Ƃł��B
���l�̏�̍D���ȂƂ���ɋǏ��I�ȍ��W��`�����ނ��Ƃ��ł��܂��B
��=2^(1/3)+3^(1/5)
����Ȃ��Ă�������Ȃ�ڍs����15�悵�Ă݂������łȂ���
f(x) = (x^3-2)^5 + (x^5-3)^3 -x^15 -180(3x^7 +9x^4 +3x^2 +2x),
f(x) = {(x-a)^5 -3} {(xx+ax+aa)^5 -3(2x+a)(x^4 +2ax^3-6aax^2 -7a^3 x+a^4) +9}�C
��_�ł̂ݔ����s�\�ȕ��f���́u�C�ӂ̓_�Ő����v�ł͂Ȃ��ł����H
���Ɓu���̓_�ł̂ݐ����łȂ��v�̂ł����H
2�Ԗڂ̎��₪������Ȃ��̂́A�����s�\�ȓ_�̂����߂��̓_�͐����ł͂Ȃ��Ǝv���̂ł������܂߂Ȃ��Ƃ����Ȃ��̂��悭�킩��Ȃ�����ł��B�߂��̓_�Ƃ����̂��悭�킩��Ȃ��ł��B
�����������₪�܂��悭�킩��Ȃ���ł�����
����:
��_�Ő����łȂ�
�Ȃ�ŋߖT�Ő����łȂ��Ƃ����I�������o�Ă����ł����H
>>531 �ߖT�Ƃ����\�����������̂�������܂��A�����s�\�ȓ_�̂����߂��̓_���A�ߖT���S�Ĕ����\�ł͂Ȃ��̂Ő����ł͂Ȃ��Ǝv�����̂ŁA�P���ɐ����łȂ��ꏊ�́u�_�v�Ƃ����\���ł����̂��^��Ɏv���܂��B
1/x��0�̋ߖT�Ŕ����s�\�ȓ_��0�ȊO�ɂ���܂����H
�����s�\�ȓ_�̂����߂��̓_�͕��ʂɐ������肦�܂�
>>532 ����_�Ő����\�Ȏ��̒�`�́u�S�Ă̋ߖT�Ŕ����\�v�Ȏ��ł͂Ȃ���
�u����ߖT�̑S�Ă̓_�Ŕ����\�v�Ȏ��ł�
���ՂȂ������\�ł���悤�ȗ̈�����������ΐ����Ȃ̂ł�
�����s�\�ȓ_�̂����߂��ɓ_��������Ƃ��āA�����s�\�ȓ_�ɐG��Ȃ��悤�ɂ��̓_�̎���ɉ~�����������͐����Ƃ������ł�
�u�S�Ĕ����\�ł͂Ȃ��v
>>537 ������_�Ő����\�Ȏ��̒�`�́u�S�Ă̋ߖT�Ŕ����\�v�Ȏ��ł͂Ȃ���
�u����ߖT�̑S�Ă̓_�Ŕ����\�v�Ȏ��ł�
���݂܂���A�S�Ă̋ߖT�Ƃ����̂͋ߖT�S�̂Ƃ����Ӗ��ŏ����܂��������m�łȂ���������Ȃ��ł��ˁB
a,b,c,d�͐��̐����ŁA
1 2 3 6| 1^3+2^3+3^3==1+8+27==36==(1*2*3)^2
1^3 + 2^3 + ����� + n^3 = (1+2+����+n)^2,�@�@�@�@(�������̌���)
�ŏ��̖�肾���ł������̂œ����������Ă��������B
�R�[�V�[���[�}���̊W�������藧���ǂ������ׂ邾���ł����
����͕�����܂������͎̉��M�������ł��B
�����Ȃ�_�ł������łȂ��A�Ƃ͂ǂ������Ӗ��ł����H
�u��z��C f(z)�͐����v�łȂ�
���݂܂���A�Ⴂ���킩��Ȃ��ł��B�B
���͂��Ȃ������������Ă�悤�Ɍ������ł����ǁA����͈Ⴂ�܂���
>>551 ���݂܂���A������܂����B
�����Ǝv���܂��B
�����ȓ_�������Ƃ����Ӗ��ł��B
>>552 �����Ȃ̂ł����H
���R�͂Ȃ�ł��傤���B
����_�ɂ����Ċ��������ł���Ƃ͂ǂ̂悤�Ȃ��Ƃł����H
�ߖT�̈�̓����S���̓_�Ŕ����\�Ƃ������Ƃł����H
���̋ߖT�́h����ߖT�h�ł����H�h�S�Ă̋ߖT�h�ł����H
>>557 ����ߖT���Ǝv���܂��B
�߂��Ⴍ���Ꮼ�����ߖT������Ă����Ŕ����\�Ȃ琳�����Ǝv���܂��B
�Ȃ�0�ȊO�̓_�Ő����łȂ��Ǝ咣����̂͂��������ł���˂�
���������Đ��ɉ����ċߖT���������S���Ŕ����\�����琳���Ƃ������Ƃł����H
>>562 �������̖���y=�}x�̐��̏�ɔ����\�ȓ_������ł���Ǝv���̂ł������̐��ł��B
�����������ꎩ�̊Ԉ���Ă邩������Ȃ��ł����B
>>563 �Ⴂ�܂���
0�ȊO�ł͔����ł���͂��ł���
>>564 ���Ƃ�������͂�I����Ă܂��ˁB
>>519 ���A�������c
������Ăǂ�����ē��o�ł���̂ł��傤���H
>>568 f(x) = {(x-a)^5 -3} {(xx+ax+aa)^5 - 3(2x+a)[(xx+ax+aa)^2 - 9aa(xx+ax+aa) + 9a^4] + 9},
P(x,y)=(��+r*sin��,1+r*cos��) (0���Ɓ�2��)�Ar>1�Ƃ���ƁA
>>572 ����͂����肸�\����܂���
�Ȃ�����͐����W���ɂȂ�Ɨ\�m�ł����̂ł��傤���H
>>573 = 2[... ...](0��t)
= 2t - 4r.sint + rr.t + tt/tant
= 2t - 4t + (t/sint)^2 t + tt/tant = ...
�ł��ˁB
>>575 ���[�܂����[
���肪�Ƃ��������܂��I
�������Ă��C�Â��Ȃ��̂ŏI����Ă܂���^^;
>>572 X = x-a��,�@X~ = x-a��~,�@�ց�1 ��1��3�捪
�Ƃ�����
XX~ = xx+ax+aa,�@(X-X~)^2 = -3aa,
���iX^5 - 3)(X~^5 - 3)
= (XX~)^5 - 3[(X)^5 + (X~)^5] + 9
= (XX~)^5 - 3(X+X~)[(X^4) -(X^3)(X~) +(XX~)^2 -X(X~)^3 +(X~)^4] + 9
= (XX~)^5 - 3(X+X~)[(XX~)^2 + 3(XX~)(X-X~)^2 + (X-X~)^4] + 9
= (xx+ax+aa)^5 - 3(2x+a)[(xx+ax+aa)^2 - 9aa(xx+ax+aa) + 9a^4] + 9,
�Ȃ������W���ɂȂ��ł��傤�H�H�H
>>577 >>577 �͗ʂ����肸�\����܂���
f(x) = {(x-a)^5 -3} {(xx+ax+aa)^5 - 3(2x+a)[(xx+ax+aa)^2 - 9aa(xx+ax+aa) + 9a^4] + 9}
���̏�Ԃ���x�̎��̕\���ɖ�������a���܂܂�Ă���̂�
���������x�ɂ��Ă̑������ɂ���ƑS�Đ����W���ɂȂ�̂��������Ƃ����̂�������܂���ł���
�ŏ��������Ƃ����̂�����̂ł��ˁA�����Ă݂܂����肪�Ƃ��������܂�
>>577 ����Ȃ�łǂ��ł����ˁB
a1 := a,�@a2 := a.��,�@a3 := a.��~
(x-a1)(x-a2)(x-a3) = x^3 - 2
��{�Ώ̎�:
u1 = a1 + a2 + a3 = 0
u2 = a1.a2 + a2.a3 + a3.a1 = 0
u3 = a1.a2.a3 = 2
f(x) = ((x-a1)^5 - 3)((x-a2)^5 - 3)((x-a3)^5 - 3)�@{�W����a1,a2,a3 �̑Ώ̎�}
= F(x, u1,u2,u3)�@{(�����W��)���ϐ�������}
= F(x, 0,0,2)
�Ώ̎��͕K����{�Ώ̎��ŕ\����́H ���ꂪ�����W���ɂȂ�́H���ĕӂ��
�����O�}�`���g���Ί��o�I�ɕ�����B
f(a+b) = ((a+b-a)^5 - 3)(...)(...) = (b^5 - 3)(...)(...) = 0
>>578 �ŏ��������ł��鎖�͂ǂ�����Ď������ł����H
>>579 ,580
�ŏ��������ɂ��ẮA�K���A���_�̒m�����K�v�ɂȂ�B
�����������W���ł��邽�߂ɂ́A�K���A�Q�ɂ���p�ŕs�ςł��邱�Ƃ��K�v�B
���̂��߂ɂ́A�������́A�����̑S�Ă̒u�������Ƃ��Ď����Ȃ���Ȃ�Ȃ��B
��́A�{�l�ɔC����B
���̍ŏ��������� >>578 >>519 �ȉ��̖��ŁA�����藝���g���ĕӒ�a,b�Ɗp���A�������т��͕̂�����̂ł����A�^��(1-cos��)/(1-cos��)���ǂ����т���̂��킩��܂���B
>>583 (1-cos��)/(1-cos��) = ( sin(��/2) / sin(��/2) )^2
b/a�@�F�@��(1-cos��) / ��(1-cos��)�@�F�@��/��
>>580 �k���l�@�Ώ̑������͊�{�Ώ̎��̑������ŕ\�킹�A�W���͐����ł���B
{a1,a2,a3} �̊�{�Ώ̎���
�@s = a1 + a2 + a3,
�@t = a1a2 + a2a3 + a3a1,
�@u = a1�a2�a3,
�ł���B
�Ώ̑����� g(a1,a2,a3) �� (a1)^c1�(a2)^c2�(a3)^c3 �̌`�̍��̘a
k���̍� ( c1+c2+c3 = k) �݂̂��܂ޑΏ̎��ɂ��Ď����悢�B
{c1,c2,c3} �����������܂Ƃ߂ėނƂ��Ac1��c2��c3 �ő�\����B
�����̂����Ac1���ő�̗ނ�I�ԁB
2�ȏ゠��Ƃ��́Ac2���傫���ނ�I�ԁB
c3 = k-c1-c2 �Ō��܂�B�i������ł������ނƂ���)
�Ώ̎�g��k����
�@s^(c1-c2)�t^(c2-c3)�u^c3
���܂ށB���������������
�@g(a1,a2,a3) - s^(c1-c2)�t^(c2-c3)�u^c3
���Ώ̎��ł��邪�Ag���ア�B
2�Ԗڂɋ����ނɂ��Ă����l�Ƃ���B
������J��Ԃ��Ƌ����ނ�������Ă䂫�A�Ō��0�ɂȂ�B(�I)
http://mathtrain.jp/symfundamental >>580 >>586 �́`�`���肪�Ƃ��������܂��B
����͂悭�l����Ε����肻���ȋC�����܂��l���Ă݂܂��B
>>580 x,y,z�͎��R���ŁA
2(LHS-RHS)/(x+y+z)=(x-y)^2+(y-z)^2+(z-x)^2=0
���ꂪ�킩��Ȃ��ł�
�����Ă��������܂���
��Βl���傫���Ȃ肻���Ȑ����ł�����Ƃ����Ă���̂ł���
�ǂ̂悤�Ȑ����ł�����悢���킩��܂���
���Ƃ��̖��Ɍ��炸�����̂ł�����ƌ����̂̓_���Ȃ�ł����H
>>592 �����܂���
�����Ȃ������Ă��������܂���
>>593 ���@�Ђ����A�̌`�̋Ɍ��ŁA
�オ����ŁA
�ǂ����������ɑ傫���Ȃ��Ă����A
�@/�A���Ɍ���1�ɋ߂Â��Ă����ꍇ�A
�ق�100���L�����ʼn����܂��B
���̏ꍇ�����邾���ł͉����Ȃ��ł��B
�@/�A��1�Ɏ������Ă����Ƃ������Ƃ́A
�@�[�A�̎��́A���ł������Ă�������~�[���̌`�ɂȂ邩��ł��B
���̖��̏ꍇ�́A
(��nn+4n+5 )+ n�ꕪ�q�ɂ�����Ɖ����܂��B
>>596 �����܂����I�I�I�I�I�I���肪�Ƃ��������܂��I
>>591 >>593 �@[�U]�@�Ɍ� lim[n����] (��{n^2 +4n+5} - n)�@�����߂�B
(����)
n^2 +4n +5 = (n+2)^2 + 1,
������@
��{n^2 +4n +5} - (n+2) = 1/(��{n^2 +4n +5} + n+2)�@���@0�@
�k�����l
���肢���܂�
>>600 �������x������Z��荂���Ƃ����̂̓X�����O�ł���
���w�̋K��ł� 2x == 2 * x
��肽�����Ƃ͂킩�邯��
8/(2(2+2)) ����
16��������ǂ����悤������16
>>600 a(��b)�Ƃ����`�ŏ����ꍇ�A�����a*b�Ƃ��ĕs���Ȉ�̂̐��ƌ��Ȃ��̂Ő�Ɍv�Z����B
8��2�~(2�{2)�@����Ȃ�16�Ƃ������߂��ł��邩��
���߂��ł��������
ab == a * b �������Ƃ��邪
>>599 �k�����l
x��0 �̂Ƃ�
�@��(xx+a) - |x| = a/(��(xx+a) + |x|) �� a/(2|x|),
8/2*4
w(y,t)�Ɋւ���Δ���������
>>607 ���ꃊ�A�����E���ƕ��s�Ɋ���Z�������
�v���O�����\�L���`���I�Ȑ��w�\�L�قǖ����ł͂Ȃ��Ƃ����͓̂���
>>607 > 8/2*4
>
> ���ꂾ�Ɖ��߂̗]�n������ł���
�Ȃ��B
> �ɂ���ĕς��A����K���͂Ȃ�
���ʂ��Ȃ��ȏ㍶���珇�ɉ��Z������肷��B
>>603 >>607 ���肪�Ƃ��������܂��B
�������肵�܂����B
>>601 >>602 ����H���߂�Ȃ����܂��܂��킩��܂���
����u�^�v�̒�`���B�������獶���珇�Ƃ͌������
>�ɂ���ĕς��A����K���͂Ȃ�
>>614 ����Z�̃G�C���A�X�ł���
>>616 ������A�u���ɂ��v���Z�Ȃ̂����B��
>>617 / == ��
���Ƃ��ƉE���̕�����
100������Ƃ����������v���O�����Ŏg���Ȃ���������ł�
����Z�Ƃ��Ďg���ɂ͕s�K����������
���w�̕����s�̕��s�Ȋ���Z�\�L�Ɏ��� / �����肠�Ă�ꂽ�B
�Ȍ������烊�A���̕��ł� ����� 1/2 �Ƃ������悤�ɂȂ���
�l���v�Z�ӊO�̐V�����Z�p����`���ꂽ�̂ł͂Ȃ�
���̃G�C���A�X
������������킵������������ЂƂ̓��x���Ⴂ�ł����A����킵�������ɔ������悤�Ƃ���l�������܂����x�����Ⴂ�̂ł���
8/2(2�{2)�ł�8��2(2�{2)�ł����ʂ�16
�Ȃr�ꂳ���Ă����܂���B
>>622 ���������Γ���������ƍl����̂�����������ł���
�l�ԒN�ł������������܂���ˁH
���̎��͏��������ł�
����킵���������߂��悤�Ɠw�͂��邱�ƂɂȂ�̈Ӗ�������܂���
�̌������Ȃ���Ε��z�@���͐������Ȃ�
�i2�j�܂ł͕�����܂����B�i1�j�Ɠ������Ƃ�������������ł����B
�����]�X�͊W�Ȃ��ł���
>>622 ���ǂł��ˁA��������ăl�b�g�ʼn��N���l�^�ɂ���Ă���Ă��Ƃ����̎����s�e�ȏ����������Ă��Ƃ̈�Ԃ̏؋��Ȃ�ł���
�����Ƃ������R�t�����ł���Ȃ�Ƃ����ɉ������Ă�͂��ł������
���ĂȂ��Ƃ������Ƃ́A�N���������v�Z���@���߂ĂȂ����A�����炱�������������͕���킵�������ŏ����ׂ��ł͂Ȃ��Ƃ������ƂȂ�ł�
�̒�`�������������ɕ��z�@�����g������C�J�T�}
�_��Q�_�̋��ȏ���2(2+2)�Ƃ������L�@�̒�`�Ȃ�Ă���܂����H
>>619 ������u���ɂ��v���Z�Ȃ̂����B�������Ă邾��
>>631 4x �� 2x
����������肠�Ȃ��Ȃ�ē����Ă���ł����H
�y���w�z120x=y�̂Ƃ��ɂ�����x��y�̒l�����߂�
http://2chb.net/r/news/1564744346/ >>632 ���ꂪ���߂Ă���
2x^2
��������̕���ł͕ێ琫�̒Ⴂ���������͂��ׂ��ł͂Ȃ�
�Ɠ�����
>>635 ���w�̃e�X�g�͂����_��������������ł��傤��(��)
>>636 ���w�̂Ƃ��ɂ� nxn �s�̋t�s��������Ă���
n�̓_��ʂ� n-1���̎��������Ă�
������ >158 �������Ă����̂͒��w�̂Ƃ���
���Ԃ���{�S1��������Ȃ����H
�ȗ������X�}�[�g�ȏ�������������������
�ʔ��������o�J������
�����猾��������u���ߎ���v����
����
>>604 �̋K�������m����
>>638 �ł͂��̂悤�ɏ����ׂ��ł���
8��2(2�{2)
������������킵���������͂��������܂����
���܂ł��_���������̂͋��ȏ��ɂ��̂悤�ȕ\�L�����݂��Ȃ����炾�Ǝv��
/�Q/�Q/�l�l_/�Q/�Q/�Q
/�Q/_�i�Q)_)/�Q/�Q/�Q
/�Q/_�i_(�Q)/_�O
>>610 /�Q/_�i^_^)) __/__/__
/�Q/__(������__/�Q/�Q
/�Q/��ރ҄�_/__/__/__
/�Q/�Q/�Q���/�Q/�Q/�Q/�Q/�Q/�����c�c��_/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q
>>634 �O�p���̑̐σ}�W���X�����̂Ƀn���l���q�h���ɂȂ�����B/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q
���w���Ƃ��܂�ێ琫�Ɍ��y����邱�Ƃ͏��Ȃ�����
>>644 ���ꂾ��s�Ƌ�ʂ��Ȃ��Ȃ������H
>>645 ��������
>>646 >>644 > z �������������Ƃ��� ���ォ��E���Ɍ������ĂȂȂ߂ɐ�������Ă�
�u��������Ă�v�Ƃ͐���lj����Ă���A�Ƃ����Ӗ��ˁB
>>625 �ǂȂ������̖��́i3�j�����肢���܂��B
���R���Ƃ́A���ʂ�\�����ł���ƌ������ˁB
>>649 �C���Ɏg���鐔���ȁH
0�x���}�C�i�X7�x�����邵
�����A�C����10.7�x�Ƃ��������g���邩���
>>649 1 ��+- �ŕ\���ł��鐔�ł���
�������镨���̃J�E���g�Ɏg����
-200���̐Ԏ��Ƃ�
50���̍����Ȃ�
>>625 ,
>>648 { (x+y+z)/3 }^2 �� (xx + yy + zz)/3�@(�� Jensen�s���� (�������������� x=y=z ) )
�@= { (x+y+z)^2 - 2 (xy+yz+zx) } / 3
0 �� (x+y+z)^2 - 3(xy+yz+zx)
0 �� {(x+y+z)^3 - 3(xy+yz+zx)(x+y+z) + 3xyz } - 3xyz�@(�� 0 < x+y+z )
0 �� x^3 + y^3 + z^3 - 3xyz
�� x^3 + y^3 + z^3 �� 3xyz
x<y<z �̎��ɓ������������邱�Ƃ͂Ȃ��B
(2)���g�����͕������
�ʔ������̖ʔ�����@�������������I�I�Ȃ����Ȃ��́H
������������o���Ċ��ł�̂��݂�Ȕ����Ă�́A�킩��Ȃ����Ȃ��c�c�c
�s�тȂ���P�����̎�舵�����S���킩��Ȃ��̂ʼn������̕��j�������Ă�������
B_n��R^n���Borel�W���̂ł�
�������������� x=y=z �Ɖ��肷��
�����܂���
>>608 >>625 �@>>648 >>590 >>658 608�ł�
��낵����ǂ̂悤�ɉ����̂������Ē����܂��H
�ϐ������̌`�̔g���������Ȃ������̂ł����A����������ɏ��߂Č���p�^�[���ł��B
>>659 �NjL
���̕��������M�`���������Ƃ������̂��Ƃ����ׂ̂ė������܂����B
https://whyitsso.net/math/differential_equation/diffusion_equation4.html ���̃T�C�g���Q�l�ɉ������̂ł����A�t�[���G�t�ϊ��������Ƃ̐ϕ�����肭�ł����܂��Ă��܂��܂���
n���������s��P��P^2=P����R^n��Im P��Im P�̕��Ԃ̒��a�ŕ\�����Ƃ�P�͑Ώ̍s��ł��邱�Ƃ������B
>>661 �ԈႦ�܂���
Im P �� (Ker P�̕���) �̒��a
�ł�
>>661 ���x�����݂܂���B����ǂ݊ԈႦ�Ă܂����B
��������
n���������s��P��P^2=P����Im P��Ker P���������AIm P��Ker P={0}�̂Ƃ�P�͑Ώ̍s��ł��邱�Ƃ������B
�Ƃ������ł��B
�X�������Đ\���킯�Ȃ��ł��B
>>659 >>660 w(y,t) = sin(ay+b)g(t)
�Ƃ����B�@�^������
�@��w/��t = ��^2 w /(��y)^2 = -aa���,
sin(ax+b) �Ŋ����
�@g '(t) = -aa�g(t),
�����������
�@g(t) = exp(-aat),
�@w(y,t) = sin(ay+b) exp(-aat),
������d�ˍ��킹��B
>>664 ImP�̔C�ӗv�f v �ɂ� �K���� R^n�̗v�f x �����݂��ā@v = P.x �Ə�����.
������� P.v = PP.x = P.x = 1.v
�܂� ImP�@�� �ŗL�l 1 �̌ŗL��ԁA
������ KerP �� �ŗL�l 0 �̌ŗL��Ԃł���.
�������ImP��KerP�͒������Ă��āA���� n=dim(ImP)+ dim(KerP) �Ȃ̂�
R^n = ImP + KerP
�܂�K���Ȓ������ɑ��� P�� diag(1,1,...,1, 0,...,0) �Ə�����. (diagonal matrix: �Ίp�s��)
P = R.diag(1,1,...,1, 0,...,0).R^t�@ (R�͉�]�s��)
����� P^t = P
P�͑Ώ̍s��ł���.
(�lj�)
>>665 > w(y,t) = sin(ay+b)g(t)
> �Ƃ����B
����͔M�`���������������Ƃ��͂�������̂������܂�݂����Ȃ��̂Ȃ̂ł����H����Ƃ��������������č���͂��̂悤�ɒu�����Ƃ������ƂȂ̂ł��傤���H
�����܂�ƌ����Ă��悢�ł��傤�B
�����܂�ƌ����Ă��悢�ł��傤�B
e�ꂪ1���̗L�����ŋߎ�����Ƃ��A�ł����x���ǂ����̂����߂Ȃ����B
>>672 ���w����1���̉ߋ����W�ɂ��������ŁA�P�ɐ����Ə�����Ă��܂����B
���l�Ƃ��Ă�e=2.718281828...�݂̂��^�����Ă��܂��B
1�������̂��ߌv�Z�ߒ���_�q�͕s�v�ł����A�ǂ����čŏ��̕�����19/7�Ɍ��܂�̂��S��������Ă��炸���_��������܂���B
>>673 ������9�Ȃ�ă��[���[�ł�����
en=m | n= 1..9, e=2.718281828
9����v�Z��������
n=3�̂Ƃ���m=7.15...�Ɛ�������0.15����ĂėL�͂�����
n=7�̂Ƃ���19.0...�Ƃ��Ȃ萮���ɋ߂�����
>>667 ���肪�Ƃ��������܂��I�����ł��܂���
>>673 �H�H�H
9�ʂ莎�����������
2.7 2.718 ���炢�܂ł̕]�����Ă���������
�_���A�I���̓_���B
���Ⴀ�i�����
�F�l���X���肪�Ƃ��������܂��B
19/7 ���� 14�{���� ����98 ���q19*14�O�オ
>>682 ���肪�Ƃ��������܂��B
����������Ă������ƂɂȂ��ł��ˁB
e�̋ߎ��l�����߂�Ƃ������̂ŁA�A������e�C���[�W�J���g���̂��Ǝv���܂������Ae�ɑS���W�Ȃ���肾�Ƃ͎v���܂���ł����B
����A�_�����B
�ߎ��\���������l��e=2.718281828...
2<e<3 �Ȃ̂�
>>684 e�̘A�����W�J�͏z���Ȃ����̂̈��̋K���������B
e = 2 + 1/(1 + 1/(2 + 1/(1 + 1/(1 + 1/(4 +����)))))
�@= 2 + [1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8, 1, 1, 10, ...]
���߂̕��́@5/2, 11/4, 19/7, 68/25, 106/39, 193/71, 299/110, 1457/536, 2721/1001, 4178/1537, 25946/9545, 49171/18089, ����
http://oeis.org/A003417 ����1���@19/7�@= 2.7143
����2���@193/71�@= 2.71831
����3���@1457/536�@= 2.7182836
>>689 �����e�Ɏ������邾���ŁA���ꂪ�~�~�ȉ��̗L�����ߎ��ōŗǂ̂��̂���^���Ă����킯����Ȃ��̂ł́H
���K�A���������炢����́H
����A�E�\�������B
����(3)��
5�̘A�����������̘a��5�̔{���ɂȂ�Ƃ���̂ł����A
������ā|2 �|1 0 1 2
�������ꍇ0�ɂȂ��Ă��܂�����A5�̔{���ɂȂ�Ȃ��Ȃ��ł����H
>>689 �A�����v�Z�œ����� x/y �͕��� y �ȉ��̗L�����̒��ł� e �̍ŗNjߎ������ǁA
�Ⴆ�� 193/71 �� ���� 99 �ȉ��̗L�����̒��ōŗNjߎ����ǂ����͗v�`�F�b�N�ł͂Ȃ��́H
�����l�����Ƀv���O�������点���
�ŗNjߎ��̐����
... , [193/71], 685/252, 878/323, 1071/394, [1264/465], [1457/536], [2721/1001], ...
�̂悤�ɑ����B(�J�M���ʂ̂͘A�����W�J�Ō����L����)
�m���� ?/72,..., ?/99 �̊ԂŋL�^�X�V�͐����Ȃ��̂����ǁA�����v�Z�ł����m�F�ł��܂�����...?
�A�����W�J�𗘗p���������́A�^�̒l�ɐU�����Ȃ���߂Â��܂��B
>>694 wiki����̎���Ŗ��m�F������farey����łł���L�����ߎ��͂ǂ��������A�����W�J�œ�����L������Ɠ����ɂȂ邭�����B
���������Ƃ��Ă̓l�C�s�A���̐����A�����W�J�Ƃ������قǃ��W���[�łȂ��b��m���ĂȂ��Ƃ�����Ƃ����̂��B
���|�[�g��o�̉ۑ�Ƃ��Ȃ�܂��������w����Ƃ��̖��Ƃ��Ă͂�����ƃ_���Ȋ������B
�������ɑ��� ||��|| = min_[n�͐���] |��-n| ���A�������̐����Ƃ̋߂���\�����̂Ƃ��āA
>>697 ����
��
||(39s+t)e|| �� abs(||0.013s|| + ||te||)
��
||(39s+t)e|| �� abs(||0.013s|| - ||te||)
�k�f�B�I�t�@���g�X�ߎ��Ɋւ���f�B���N���̒藝�l
>>699 ���ꍂ�Z���w�̔���������ɂ���
e = 2 + [1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8, 1, 1, 10, ...] �ɑ��A
>>701 > �̂悤�ɁA�A�����\���ɂ����āA�Ō�̐�������傫�����邩�A�g,1�h�������邱�Ƃɂ���āA
> ���ꂪ�傫���Ȃ鐔�ł��܂��B�i�O�҂̏ꍇ�́A�K���A�^�̒l�ɋ߂Â��܂��B�j
����Ȃ̐����łȂ��A�����ł��������邶���H
���ꂪ�~�~�ȉ����Ăׂ̂�Ȃ琳���Ȃ����Ȃ��ƃ_���Ȃ�Ȃ��́H
701 �̕��@�́A
>>687 �̃t�@���C�����̕��@���A�A�����I�ȕ\���Ɍ��������������ł��B
�]���āA�t�@���C�����Œm���Ă��鎖���A
�u���� a/b �� c/d�@���ׂ荇���Ă���Ƃ��i|ad-bc|=1�̎��j�A���(a/b,c/d)�̒��̕����̒��ŁA���ꂪ�ŏ��Ȃ̂́A(a+c)/(b+d)�v
���g���܂��B�m���ɕ����傫�����A�^�l�ɋ߂������̒T���Ɏg���܂��B
>>703 �����A������A������ł����ē�����ߎ��������אڂ���farey���2���ŋ����̂œ�������̂Ɠ����ɂȂ�Ώ\�������ǂ���͐����ȘA�����łȂ��ƌ����Ȃ��B
������
>>701 �Ō����Ă鎖�͕ʂɐ����ȘA�����łȂ��Ă��������Ă��܂��Ă�B
�����������琳���łȂ��A������������@�����邩������Ȃ����Ǐ��Ȃ��Ƃ�
>>701 �̐����ŘA�����̑ł���ߎ��ŕ��ꂪ��菬�����L�����ŋߎ��ł��Ȃ����̐����ɂ͂Ȃ��ĂȂ��Ǝv���B
>>704 �E���߂����l���A��� (a/b,c/d)�@���ɂ���B
�Ea/b �Ɓ@c/d�@�ׂ͗荇���Ă���B�܂�A|ad-bc|=1�B
��
���(a/b,c/d)���̂��ׂĂ̗L�����̕����(b+d)�ȏ�
��
���[a/b,c/d]�@�̒��ŁA���ꂪ(b+d)�ȉ��̕����ŁA���߂����l�ɋ߂����̂́A
a/b�A(a+c)/(b+d)�Ac/d�@�̂����ꂩ
�Ƃ����_���ł����A��肠��܂����H
�O������ɂȂ��Ă���Ƃ������A�����͈͂����߁A�������������Ă�������Ƃ������܂����A
�ׂ荇�������ŋ��܂ꂽ��� (a/b,c/d)�@���ɐ^�l������Ƃ������_�ŁA
���ꂪ b �� d ��菬���������S�āA���͈̔͂̊O�ɂ���̂ŁA�^�l�ɂ��߂������Ƃ��ẮA
a/b �� c/d �ɔs�k���Ă���̂ł��B
�^�l�ɋ߂����Ƃ��ẮAa/b �Ac/d�@����сA����炩��u�t�@���C����i�H�j�v�ɂ���č���镪��
�Ɍ����Ă悢�̂ł��B
�������������������̂��ȁH
����A�אڂ���farey����ŋ��߂��̊Ԃɕ��ꂪ�������L���������݂��Ȃ��̂͂����ł���B
���͐����ł͂Ȃ���������Ȃ��A�����̑ł���ߎ��œ�����㉺����̋��ݓ����͕K�������א�farey���2���Ƃ͌���Ȃ��ł���ˁH
����͐����A�����Ȃ�m���ɐ������������A�����������Ă�ł���ߎ��̎����Ă��鐫���𗘗p����Ώؖ��ł��܂����A
>>701 �ŗ}���Ă��鐫���͐����ł͂Ȃ��A�����ł������Ă��鐫���Ȃ̂ŁA��������ł���ߎ����א�farey���2���Ƃ͌����Ȃ��̂ł͂Ȃ����Ƃ����^��ł��B
>>705 ,
>>706 �������܂藝���ł��Ă��Ȃ��ĂȂ�Ȃ�ł����ǁA
> �ŗNjߎ��̐����
> ... , [193/71], 685/252, 878/323, 1071/394, [1264/465], [1457/536], [2721/1001], ...
> �̂悤�ɑ����B(�J�M���ʂ̂͘A�����W�J�Ō����L����)
���̃t�@���C����� 193/71 �̎��ɗ��� 685/252 �͕ߑ��ł���̂ł����H
�����łȂ��Ȃ�A193/71 �̎��ɗ��镪�ꂪ�R���Ȃ̂͋��R���b�L�[�Ȃ����̂悤�Ɍ�����̂ł��B
2�����R�����̂͒P�ɂP�O�i���Ɉˋ������\���ł�����B
>>707 �o�����_�Ŏg�����A2/1�@�Ɓ@3/1�́@�ׂ荇���Ă��镪���ł��B
���ꓯ�m�A���q���m�̘a�ō����@5/2�@�́A2/1�@�Ƃ��A3/1�Ƃ��ׂ荇���Ă��܂��B
�܂�A�ׂ荇���������@a/b�@�Ɓ@c/d�@��������@(a+c)/(b+d)�́Aa/b�Ƃ�c/d�Ƃ��ׂ荇���Ă��܂��B
�ׂ荇��������a/b��c/d�ŋ��܂ꂽ��Ԃ��A(a+c)/(b+d)�@�œ��A
[a/b,(a+c)/(b+d)]�@���邢�́A[(a+c)/(b+d),c/d]�ɕ����A���ڂ����Ԃ��ǂ��炩�Ɍ��肵�A����ɁA
�����悤�ȑ�����J��Ԃ����ꍇ�ł��A��ɒ��ڂ����Ԃ́A�ׂ荇���������ŋ��܂ꂽ��ԂƂȂ�܂��B
�������͂���܂���B
>>708 �@
>>701 �@�œr�����ȗ����Ă܂����A�ŏ��̏ȗ�����
2 + [1, 2, 1, 1, 4, 1, 1, 3]
�����ɁA 685/252�ł��B
https://www.wolframalpha.com/input/?i=%5B2 ;1,+2,+1,+1,+4,+1,+1,+3%5D
>>708 �����X�ł��B
��ʂɐ��̍�����Ȃ�A�����̑ł���ߎ�����Ȃ�L������͂��̖����A�����̎����l���㉺������݂ɋ���Ŏ������Ă����B
�����Ă��̘A�����������ł���Ȃ炻��2����"�אڂ���"�ɂȂ�B
�Ⴆ��2721/1001<e<1457/536
�͕��ꂪ1001�ȉ��̗L�����̍ŗǂ̏㉺����̋ߎ���^����B
����ėႦ�Ε��ꂪ5���̍ŗǂ̋ߎ����~������ΐ����A����������Αł���ߎ��̕��ꂪ�傫����6������Ƃ���܂Ōv�Z���āA���̒��ŕ��ꂪ5���̈�ԋ߂����̂������B
�����A�������Y��ɕ��Ԃ���(�����o�[�g�A�����Ƃ�)�Ȃ炤�܂������B
�ł������̗אڑQ�������������悤�Ȑ����ł͂Ȃ��A�������Ƒ������܂������Ȃ��B
���܂������Ȃ���̓I�ȗ�͒m��Ȃ����ǁB
>>712 ���̕��@�́A
>>694 �@���v�Z���Ă��ꂽ�Ƃ���́A�J�M���ʕt���̂��݂̂̂����Ƃ�����@���Ǝv���܂��B
���ӓI�Ȑݒ�ł����A�u���ꂪ400�ȉ��v���ƁA�{���̓����́A1071/394�@�ł����A
>>712 �̕��@���ƁA193/71�@�̎����A1264/465�@�ƂȂ�̂ŁA193/71�Ɓ@�����Ă��܂��̂ł͂Ȃ��ł��傤���H
e = [2; 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8, 1, 1, 10, ...] �ɑ��A
[2; 1, 2, 1, 1, 4, 1, 1]=193/71
[2; 1, 2, 1, 1, 4, 1, 1, 6]=1264/465
������A193/71�Ƃ���̂ł͖����A
[2; 1, 2, 1, 1, 4, 1, 1, k]�Ƃ��āAk=1,2,3,4,5�@�̂悤�Ȃ��̂����ɉ�����悢�Ƃ����̂��A���̎咣�ŁA
���ہAk=5�ŁA1071/394�@�������܂��B
����H���������ȁH
���A���̓~�X����
���A����A���킩�����B
�^����ꂽ�L�����@n/m�@�ɑ��A�@|ad-bc|=1,n=a+c,m=b+d�@,a/b < c/d�����B��̐������@(a,b,c,d)�@��
[a/b,c/d] �̂悤�ɕ\�L���A
>>701 �̓��e�̍ʼnE�ӂɓY���܂����B
[2;1,1] = 5/2 : [2/1,3/1]
[2;1,2] = 8/3 : [5/2,3/1]
[2;1,2,1] = 11/4 : [8/3,3/1]
[2;1,2,1,1] = 19/7 : [8/3,11/4]
[2;1,2,1,1,1] = 30/11 : [19/7,11/4]
[2;1,2,1,1,2] = 49/18 : [19/7,30/11]
[2;1,2,1,1,3] = 68/25 : [19/7,49/18]
[2;1,2,1,1,4] = 87/32 : [19/7,68/25]
[2;1,2,1,1,4,1] = 106/39 : [19/7,87/32]
[2;1,2,1,1,4,1,1] = 193/71 : [106/39,87/32]
[2;1,2,1,1,4,1,1,1] = 299/110 : [106/39,193/71]
[2;1,2,1,1,4,1,1,2] = 492/181 : [299/110,193/71]
[2;1,2,1,1,4,1,1,3] = 685/252 : [492/181,193/71]
[2;1,2,1,1,4,1,1,4] = 878/323 : [685/252,193/71]
[2;1,2,1,1,4,1,1,5] = 1071/394 : [878/323,193/71]
[2;1,2,1,1,4,1,1,6] = 1264/465 : [1071/394,193/71]
[2;1,2,1,1,4,1,1,6,1] = 1457/536 : [1264/465,193/71]
[2;1,2,1,1,4,1,1,6,1,1] = 2721/1001 : [1264/465,1457/536]
�m���_�����ĂăX�`���`�F�X�ϕ����Ă̂��łė��ē��ɏڂ����������Ȃ��܂ܗ����ꂽ����
>>720 ���Z���w�̔��������ꌩ��H
>>720 ���x���Ⴄ�����ɉ߂���
�m���_����Ȃ瑪�x�_�͊�b����
>>719 ������
>>714 ����̎w�E�ɂ͂ǂ�������́H
�ł���ߎ��̒��ɉ�������Ƃ͌���Ȃ�����A�ł���ߎ��̒��̂��Ƃ��Ε���400�ȉ��̍ŗǕ\�����킩�����Ƃ��āA���ۂ̕��ꂪ400�ȉ��̍ŗNjߎ�1071/394�����߂�ɂ͂ǂ�����́H
>>723 ���������Ă���̂��A���f���Ă���̂ł����A
>>714 ��
>>719 �����̔����ł��B
�ŗNjߎ�1071/394�́A
>> [2;1,2,1,1,4,1,1,5] = 1071/394 : [878/323,193/71]
�Ƃ��āA���ɋ������Ă܂��B
���̂悤�Ȍ����������Ȃ��悤�ɁA�Ō�̐�������Âω������Ă���̂ł��B
�i���̑��삪�A�u�t�@���C����v�ɑΉ����Ă��܂��B�j
���ʁAe = [2;1,2,1,1,4,1,1,6,1,1,8,1,1,10, ...] �ɑ��A
[2;1],[2;1,2],[2;1,2,1],[2;1,2,1,1],[2;1,2,1,1,4],[2;1,2,1,1,4,1],[2;1,2,1,1,4,1,1],...
�̂悤�Ȍ`�ŁA�ł��蕔�����A�L���Ă����܂����A
>>718 �̂悤�Ȍ`�ŁA�L�����Ƃɂ��A
��������킶��傫�����Ȃ���A�^�l�ɋ߂�����T�邱�ƂɂȂ�܂��B
��x���ȕ\���͂����̂ł����A�ēx�⑫���Ă����ƁA
>>718 ��ɏ�����Ă��镪���́A
����͏�ɑ傫���͂Ȃ��Ă��܂����A��ɐ^�l�ɋ߂Â��Ă���킯�ł͂���܂���B
�덷�̐��������]����ӂ�ŁA�덷���傫���Ȃ�܂��B
���̌�A�덷�������Ă����̂ł����A���������]���铖����ŁA�ēx�덷���ӂ���܂��B
���̌J��Ԃ��ŁA�^�l�ɋ߂Â��Ă����܂��B
�ǂȂ������̖���(5)�������Ē����܂���
(4)��b=�� ��^(1/n), c=�� (1-��)^(1/n)�Ƃ����������o�Ă�����g���̂��Ǝv���̂ł����悭�킩��܂���ł���
>>724 �����܂���B��͂�킩��܂���B
��̓I��
>>723 �̂悤�Ȑݖ�ł͘A�����W�J�̑ł���ߎ��𗘗p������@�̋L�q�ł͂ǂ��Ȃ��ł����H
k=1,2,3,4,5�@�̂悤�Ȃ��̂����ɉ�����悢�Ƃ����̂��A���̎咣�ŁA
> ���ہAk=5�ŁA1071/394�@�������܂��B
�����k���グ�Ă��������̂̒��ɕK����������͉̂��̂ł����H
���A�Ԉ�����B
>>727 ���Z���w�̔��������ꌩ��킩��
a,b�����R���Ƃ���Bax+by=1��������x,y�����݂���Ƃ�,
�O
>>730 �^��=(x^2-7x+11)^(x^2-13x+42)=1
x^2-7x+11=1�̂Ƃ��A
x=2,5�\�\�@
x^2-13x+42=20,12
�^��=1^20=1^12=1
x^2-13x+42=0�̂Ƃ��A
x=(13�}��169-168)/2
=7,6�\�\�A
�^��=(7^2-7�7+11)^0=11^0=1
�@�A���Ax=2,5,6,7
>>726 �@
>>687 �Ŏ��������@�A�܂�A�^�[�Q�b�g�͈̔͂��A��ɕ����A���̂ǂ���ɁA�ړI�̒l��
���݂��邩���`�F�b�N���A���݂�����͈̔͂��A�V���ȃ^�[�Q�b�g�͈͂Ƃ��ē�ɕ����A�D�D�D
���J��Ԃ��Ă����A�ړI�̒l���܂ޔ͈͂��ǂ�ǂ������Ă����邱�Ƃ́A�������Ǝv���܂��B
�����āA���̎��A�͈̗͂��[�Ƃ��āA�u�ׂ荇���L�����v��p���A����ɁA�͈͂��ɕ����镪��_�Ƃ��āA
�u���Ԑ��v�i��(���q���m�̘a)/(���ꓯ�m�̘a)�j��p����A�͈͂��K�肷�镪���̕���͏�ɑ傫���Ȃ�
�Ƃ��������֗̕��Ȑ���������A�u����́����ȉ��v�̂悤�ȏ������ł̒T���ɂ́A���x�悢���Ƃ́A��낵���ł��傤���H
�����āA���̕��@�ŁA�m���ɖړI��B�����邱�Ƃ���낵���Ǝv���܂��B
���̂悤�ȕ��@���u�t�@���C����v���g�������@�Ə���ɌĂ�ł��܂����B
����ɑ��A�A�����̓r���ł����p������@�́A�u�t�@���C����v�̕��@�̖��ʂȕ�����藎�Ƃ������@�ƌ����܂��B
�t�@���C����ł́A�^�[�Q�b�g��Ԃ��ɕ����A��ʂ͈̔͂����ʂ͈̔͂��������Ȃ���A�i��ł����܂����A
��ʁA���ʁA��ʁA���ʁA��ʁA���ʁA�Ɣ��]���A���đ����ɋN����ꍇ������A
��ʁA��ʁA��ʁA�D�D�D�Ɠ��������A���x�������悤�ȏꍇ������܂��B
�O�҂Ƃ��āA��\�I�Ȃ̂��A������ł���A��҂̍D�Ⴊ�ł��B
�̋ߎ��l�����߂�ׂ��A�t�@���C�̕��@���Ƃ�ƁA����i�K�ŁA[333/106,22/7]�@�ƂȂ�A���́A[333/106,355/113]
�Ȃ̂ł����A���̏�� 355/113 �́A�ɋ߂����߁A���̌�A���x�����x���A��ʂ��肪�I��邱�ƂɂȂ�܂��B
�̘A�����\�L�́A[3;7,15,1,292,1,1,1,2,1,3,1,14,...]�ł����A
�����ɂ���l�B�̓Z���^�[�����Ŗ��_�Ƃ�܂����H
>>736 ���Z���w�̔���������ɏ����Ă��ˁH
>>730 �݂����Ȗ��A���o��98�N�̊w�K�@��̓������Ǝv�����ǁA�ǂ������`���ŏo���낤�H
���̐����������Ă錊���߂Ȃ�Ƃ������A���������Ƃ���������Ƃ��Ă͈���ȋC������
>>734 ���̂������farey����̘b�͑��v�ł��B
���͗Ⴆ�A�ł�
> [2; 1, 2, 1, 1, 4, 1, 1, k]�Ƃ��āAk=1,2,3,4,5�@�̂悤�Ȃ��̂����ɉ�����悢�Ƃ����̂��A���̎咣�ŁA
> ���ہAk=5�ŁA1071/394�@�������܂��B
�̕����ł��B
�Ȃ����̌`�̘A�����\���������̂̒��ɉ�������ƒf���邱�Ƃ��ł���̂ł��傤�H
�����Ă��̒T����k=5�ŏI���ł���͉̂��̂ł����H
�����̗������킩��Ȃ��̂ł��B
>>730 �@(xx-7x+11)^(xx-13x+42) = 1,
���邢��
�@(xx-7x+11)^{(x-6)(x-7)} = 1,
>>731 �ɂ���
Case 1�F
�@xx-7x+11 = 1
�@(x-2)(x-5) = 0,
Case 2:
�@(x-6)(x-7) = 0�@(xx-7x+11��0)
Case 3:
�@xx-7x+11 = -1�@((x-6)(x-7) = ����)
�@(x-3)(x-4) = 0,
���@x = 2,3,4,5,6,7
>>739 ��̗�������Đ�����^���܂����B�悭�ǂ�ł������������̂ł����A
�u���̕ӂɖڐ������A�Ō��10����Â��炵�Ȃ���A�v�Ə����Ă��܂��B
[2;1,2,1,1,4,1,1,6,1,1,8,1,1,10]�A[2;1,2,1,1,4,1,1,6,1,1,8,1,1,9]�A[2;1,2,1,1,4,1,1,6,1,1,8,1,1,8]�A
[2;1,2,1,1,4,1,1,6,1,1,8,1,1,7]�A[2;1,2,1,1,4,1,1,6,1,1,8,1,1,6]�A[2;1,2,1,1,4,1,1,6,1,1,8,1,1,5]
�ƍŌ�̐����������Ȃ���A���ꂪ5���Ɏ��܂�[2;1,2,1,1,4,1,1,6,1,1,8,1,1,5]���������̂ł��B
�����Ă��ꂪ�A�u���v�����Ƃ͒f���Ă��܂���B�����܂Ō�₾�ƁB�����āA���̌����A���x���A
[2;1,2,1,1,4,1,1,6,1,1,8,1,1]��舫��������A�̂Ă邱�ƂɂȂ�܂��B
�Ȃ��A[2;1,2,1,1,4,1,1,6,1,1,8,1,1,4]����A[2;1,2,1,1,4,1,1,6,1,1,8,1,1,1]�܂ł́A
[2;1,2,1,1,4,1,1,6,1,1,8,1,1,5]���A���x���Ⴂ���Ƃ��m���Ȃ̂ŁA�`�F�b�N����K�v�͂���܂���B
>> �����Ă��̒T����k=5�ŏI���ł���͉̂��̂ł����H
k=5�ŏI�������̂ł͂���܂���Bk=6�ɑ���������̂��A����̏��������̂�T���̂ŁA
�^�����k=5���`�F�b�N�����̂ł��B
�����ɂ���ẮAk=4,3,...��k�̒l�������ă`�F�b�N���܂����A���̕K�v�͂���܂���ł����B�B
>> �Ȃ����̌`�̘A�����\���������̂̒��ɉ�������ƒf���邱�Ƃ��ł���̂ł��傤�H
�J��Ԃ��ɂȂ�܂����A�f���ē����܂���B���Ƃ��Ĉ����܂��B���R�́A�����ɕ����傫�����Ȃ���^�l���܂�
�͈͂����߂�t�@���C�̕��@���A�t�����ɕ]�����Ă��邱�Ƃ��w�E����A�[�����Ē�����ł��傤���B
�O
>>733 �lj��B
�^��=(x^2-7x+11)^(x^2-13x+42)=1
x^2-7x+11=1�̂Ƃ��A
x=2,5�\�\�@
x^2-13x+42=20,12
�^��=1^20=1^12=1
x^2-13x+42=0�̂Ƃ��A
x=(13�}��169-168)/2
=7,6�\�\�A
�^��=(7^2-7�7+11)^0=11^0=1
x^2-7x+11=-1�̂Ƃ��A
(x-3)(x-4)=0
x=3,4�\�\�B
x=3�̂Ƃ��Ax^2-13x+42=9-39+42=90(����)
(-1)^90=1
x=4�̂Ƃ��Ax^2-13x+42=16-52+42=6(����)
(-1)^6=1
�@�A�B���A
x=2,3,4,5,6,7
��(1250²+n³)�������ƂȂ�悤�Ȏ��R��n�����ׂċ��߂Ă�������
�O
>>742 ���̚k�o���Â�����Ȃ�B
>>743 (-.-)�ݸ���...
��(1250^2+125^3)=1875
n=125
O���S�Ōʂ̒���R��^�ɂ����āA����_P��A����B�܂œ������ɁA��AP�̒�����x�̂Ƃ���AQ�̒������Ax�ɂ����Ƃ���f(x)�Ƃ��܂��B(AP>AQ)
���̎��AAQ���ʂ�ʐ�(�ΐ�����)�́Af(x)���ǂ̂悤�ɒ�ϕ�������߂��܂����H
Integral[0,R] f(x) dx
�ŗǂ��̂ł��傤���H
�ȒP�Ɍ����ɍ��W�ɂ����āA�ɂ���̋������p�x�ő������̒����Ɉˑ�����o�[�W�����ł�
>>736 ���͂����ɂ��钆�ł͑������\�ȕ����Ǝv���܂���
���N�������_�ł����B
>>740 ������Ă���ȊO����ł����ˁH
�O
>>746 >>747 �Ⴄ�����₯�ǁA
��`���O�p�`�ƌ��āA
����x�̌ʂ��ׂ�������x��0����R�܂ő����W�߂����̂��ӁA
�ʂ̒���x�ɑ���ΐ������̌af(x)�������Ƃ���ƁA
�O�p�`=(1/2)�~��Ӂ~����
f(x)�̐ϕ�����F(x)+C�Ƃ���ƁA
�ΐ������̖ʐ�
=(1/2)��[x=0��R]f(x)dx
={F(R)-F(0)}/2
0<x<���Œ�`���ꂽ��f(x)�ŁA
>>725 725�ł�
P(k1T_n <��<k2T_n)=P(��/k2<T_n<��/k1)=P(T_n<��/k1)-P(T_n<��/k2)=1/(k1)^n - 1/(k2)^n�ƕό`��
1/(k1)^n - 1/(k2)^n=1-���̏����̂���k2-k1���ŏ��ɂȂ�悤��k1,k2�����肷��悢
�����܂ł͂ł����̂ł��������ŋl�܂��Ă��܂��܂����B����Ƃ����j���Ԉ���Ă���̂ł��傤���H�ǂȂ����������肢�����ł��B
�����l(x)��0�ɂ͂Ȃ�Ȃ�����
�u�P���I��f(x)>0�v���āA�|�G���̃j���[�E�F�[�u�������H
>>743 n��25�̔{���̂Ƃ���
�@n = 25x >0
�@x^3 = y^2 -100
(Mordell equation, Bachet equation, Bachet-Mordell equation �Ȃ�)
�������́ix, y) = (-4,�}6)�@(0,�}10)�@(5,�}15)�@(20,�}90)�@(24,�}118)�@(2660,�}137190)
http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q12140152827 >>749 ��.�Z.��.�w.��.��.��.��.��.��.���Ă݂�
>>755 �������������������ĉ������B
���Ɖ����łȂ��čŏ��l�����݂���悤�ɂł��܂���
>>758 ���Z���w�̔�.��.����.��ɕ��傠��̂�
������������������
>>759 ����������l�K�L�������Ă�悤�ɂ��������Ȃ��B
>>760 ��w�v���o���Ȃ��A��������
(2)������������
�P���I��f(x)>0���Č������A��a���o����l�͊m���ɂ��邾�낤��
>>751 ���������\�����ł̓_���B
�������A���܂Ō����������B
�O
>>750 >>760 0��x��y��2��xy���ʂɐ}������ƁA2�ӂ�2�̒��p�ӎO�p�`���`����B
���_��(0,0),(0,2),(2,2)
z=3x^2-xy-2x+y+1
=(3x^2-2x+1)-(x-1)y
=(3x-1)(x-1)-(x-1)y
=(x-1)(3x-1-y)
xy���ʂ�x=1��y=3x-1�̃O���t��`���A����2�{�̒�����̓_(x,y)��z=0���B
���p�ӎO�p�`���̂������̓_���ɂ�݂Ȃ���Az�̒l�ׂ�ƁA
(x,y)��z=(x-1)(3x-1-y)
(0,0)��z=1
(0,1)��z=2
(0,2)��z=3
(2,2)��z=3
(1,2)��z=0
(1,1)��z=0
(1/2,1/2)��z=0
(2/3,2/3)��z=-1/9
(3/4,3/4)��z=-1/8
(4/5,4/5)��z=-3/25
���݂̎b��ŏ��lz=-1/8
>>751 g(x) = -(1-cosx)/(x^3) - 1/(x^100)
G(x) = -��_(x,��)g(t)dt
f(x) = xG(x)
�Ƃ����Af��4�̐�����S�Ė��������AL�̍ŏ��l�����݂��Ȃ��B
�i�������A�ڐ���x���̌�_�����݂��Ȃ��ꍇ��L=���ƒ�߂�j
(C1)(C4)�͖��炩�B�I�[�_�[�ׂ邱�Ƃ�(C2)(C3)���킩��B
�_(a, f(a)) �ɂ�����ڐ��̕�������
y = (ag(a)+G(a))(x-a) + f(a)
= (ag(a)+G(a))x - (a^2)g(a)
�ł��邩��A�_A��y���W�͏�ɐ��ł���A�X�� a��+�� �̎� 0 �Ɏ������邱�Ƃ��킩��B
�܂��Aa=2��n �in�͐��̐����j�̎��A�_B��x���W��
(a^2)g(a)/(ag(a)+G(a))
= (a^(-98))/(a^(-99)+G(a))
= O(1/(n^96))
�ƂȂ邩��An��+���̎� 0 �Ɏ�������B
�ȏォ�� L(x) �͏�ɐ��ł��� liminf(x��+��)L(x)=0 �ł��邩��AL(x)�̍ŏ��l�͑��݂��Ȃ��B
>>760 2�E3�@x,y �� 0��x��y��2 �����ĕω�����Ƃ��A
�@z = 3xx -xy -2x +y +1 �̍ŏ��l�����߂�B
>>762 z = 3xx-2x+1 + (1-x)y,
(i) 0��x��1 �Ȃ�A
�@��z��y�Ɋւ��ĒP�������B
�@����ā@z �� 2xx -x +1 = 2(x -1/4)^2 + 7/8 �� 7/8,
(ii) 1��x��2 �Ȃ�A
�@��z��y�Ɋւ��ĒP�������B
�@����ā@z �� 3xx -4x +3 = (x-1)(3x-1) +2 �� 2,
����āA�@(x,y) = (1/4,1/4) �Ƃ����Ƃ��� z=7/8 ���ŏ��l�B
n�������s��A�́Ai+j=k�̂Ƃ�a_ij=k�ł���(1≤i≤n,1≤j≤n)�B
�O
>>766 ���m�F�B
>>760 0��x��y��2��xy���ʂɐ}������ƁA2�ӂ�2�̒��p�ӎO�p�`���`����B
���_��(0,0),(0,2),(2,2)
z=3x^2-xy-2x+y+1
=(3x^2-2x+1)-(x-1)y
=(3x-1)(x-1)-(x-1)y
=(x-1)(3x-1-y)
xy���ʂ�x=1��y=3x-1�̃O���t��`���A����2�{�̒�����̓_(x,y)��z=0���B
���p�ӎO�p�`���̂������̓_���ɂ�݂Ȃ���Az�̒l�ׂ��B
(x,y)��z=(x-1)(3x-1-y)
(0,0)��z=1
(0,1)��z=2
(0,2)��z=3
(2,2)��z=3
(1,2)��z=0
(1,1)��z=0
(1/2,1/2)��z=0
(2/3,2/3)��z=-1/9
(3/4,3/4)��z=(-1/4)(9/4-1-3/4)
=(-9+4+3)/16
=-1/8
(4/5,4/5)��z=-3/25��-1/8
�ŏ��l�̌��z=-1/8�����A
x=y=3/4��
z=3x^2-xy-2x+y+1
�ɑ������ƁA
z=3(3/4)^2-(3/4)^2-3/4+1
=2(9/16)+1/4
=11/8��0����Ȃ��B
�v�Z�ԈႢ�̉\��������B
����=0�̂悤�Ȍ���͂��ق����B
���Ƃ��Ėʔ������ǂ����Ƃ��A����X���ɖ��o�肵�Ăǂ��Ȃ�Ƃ������邯�ǁA�����������̕��͂���z���g�ɐ��w�^�ʖڂɕ�����������̂��₢�l�߂����Ȃ��ȁB
>>769 ��k���ǂ���������Ă�̂��킯�킩���B
���ɔC�ӂ�k�ɂ��Ă��낤���ǁA����Ȃ�a_ij=i+j�Ə������������Ȃ̂ɁB
>>767 > �ȏォ�� L(x) �͏�ɐ��ł��� liminf(x��+��)L(x)=0 �ł��邩��AL(x)�̍ŏ��l�͑��݂��Ȃ��B
L(x) ���� AB �̒����Ȃ���A��� x < L(x) �ɂȂ�̂ƈႤ�́H
����Ȃ�� liminf(x��+��)L(x)=0 �ɂȂ�H
���͎̂������B
n�������s��A��i�sj��a_ij�́Aa_ij=i+j����(1≤i≤n,1≤j≤n)�B
>>775 n=1, 2 ���Ɛ����s�� (�ȒP�Ɋm���߂���)
n��3 �ł� ���s��
a_{i}{j} -2 a_{i+1}{j} + a_{i+2}{j} = (i+j) - 2.(i+j+1) + (i+j+2) = 0
����ĘA�������R�s�͕K�����^�]���ɂȂ邩��B
>>776 �f���炵��
n≥3�ŗl�q���ς�邱�Ƃ��Ӑ}�����o��ł���
>>778 �u������Ȃ����v����������Ȃ������̂���...
�N�ɂ͎��]������B
�O
>>771 0��x��y��2�\�\�@
��xy���ʂɐ}������ƁA2�ӂ�2�̒��p�ӎO�p�`���`����B
���_��(0,0),(0,2),(2,2)
z=3x^2-xy-2x+y+1
=(3x^2-2x+1)-(x-1)y
3x^2-2x+1�̈����������܂������Ă��B
z=3x^2-xy-2x+y+1
=3x^2-(y+2)x+y+1
z=3{x^2-(y+2)x/3}+y+1
=3{x-(y+2)/6}^2+y+1-{(y+2)/6)}^2
�������̎�x=(y+2)/6���@�̂ǂ͈̔͂ɂ��邩�ŏꍇ��������B
(y+2)/6��0�̂Ƃ��A
z�̍ŏ��l��x=0�̂Ƃ��A
z=y+1
y=0�̂Ƃ��A
z=1�\�\�A
0��(y+2)/6��x�̂Ƃ��A
-2��y��6x-2
z�̍ŏ��l��x=(y+2)/6�̂Ƃ��A
z=6x-2+1-3{(6x-2+2)/6}^2
=-y^2/12+2y/3+4/3
=-(1/12)(y-4)^2+4/3+4/3
=-(1/12)(y-4)^2+8/3
y=2�̂Ƃ��A
z=-(1/12)(2-4)^2+8/3
=-1/3+8/3
=7/3�\�\�B
x��(y+2)/6��y�̂Ƃ��A
6x-2��y,2/5��y
z�̍ŏ��l��x=(y+2)/6�̂Ƃ��A
z=y+1-(1/12)(y+2)^2
=-(1/12)(y^2+4y+4-12y-12)
=-(1/12)(y^2-8y)+2/3
=-(1/12)(y-4)^2+2/3+16/12
=-(1/12)(y-4)^2+2
y=2/5�̂Ƃ��A
z=-(1/12)(2/5-4)^2+2
=-(1/12)(-18/5)^2+2
�Ȃ������ƈႤ�B
y��(y+2)/6��2�̂Ƃ��A
��2��(y+2)/6�̂Ƃ��A
�܂�����2�͈͂��邯�njv�Z����������ŁA������z�̒l�̕��z�����Ă��A���Ƃ��ć@�͈̔͂�˂��钼���A
x-(y+2)/6=0���Ȃ킿y=6x-2�̐���̓_�����߂�B
z�̍ŏ��l�́A
x=y=2/5�̂Ƃ��A
z=3(2/5)^2-(2/5)(2/5)-2(2/5)-2(2/5)+(2/5)+1
=3(4/25)-(4/25)-2/5+1
=8/25-10/25+1
=23/25�\�\�C
�@�A�B�C���A
z�̍ŏ��l=23/25
y�ɂ���1���Ȃ̂�y=x��y=2�ōő�
�O
>>781 (x,y)=(2,2)�̂Ƃ��A
z=7�ł����炭�ő傾�Ǝv���B
(x,y)=(0,0),(1/2,1/2)���Ƃ���z=1������A
(x,y)=(1/4,1/4)���������ɉ������B
(x,y)=(1/2,1)�́Az=5/4
(x,y)=(0,1),(1,1)�͂Ƃ��ɁAz=2
(x,y)=(1,2)�̂Ƃ��Az=4
�O
>>783 23/25�͐ɂ��������B
7/8�̂ق����������ɂ�����Ƃ����������B
(x,y)=(1/4,1/4)�ŗ���Ƃ͂ȁB
�d�ϕ��ɂ���
>>785 �Ώ̐���p����~�c�c�̂Ƃ����/2�ł�
>>785 ���ȉ������܂����B
�ϕ��͈͓I�Ɂ���O���Ă͂����Ȃ��ł��ˁB
�Ȃʓ|��������
�O
>>784 �������A��ɓʂ����ɉ����ŏꍇ��������Ƃ������Ă��ȁB
����Ԗ������Ă��݂܂���ł����B
>>788 �ŏ��̎O���P������ł����̂ł́H
>>792 �����ł��ˁB��{k=3,n} (2^3) C{k-1,2}*(2*n-3)! = ... = (4/3)n(n-1)(n-2)(2n-3)!
( n=3 �� (1) �ƈ�v���܂� )
>>791 �̌㔼�͖Y��Ă�������...
��̊��S�������݂��邩���Ȃ��������Ă���
��̊��S�������݂��邩�ǂ����܂��������ĂȂ����Đ�����ˁB�Ȃ����킩�肻���Ȃ�����
��̊��S���Ȃ�ĂȂ�����B�O>>789 �Ȃ��ȁ`���B����Ȃ̂���킯�ȁ`��!!�@���͂͂͂́c�c >>796 �܂��ɃX���^�C�ʂ�̘b��ɂ͈Ⴂ�Ȃ�w
�uy��f(x) �� y��f⁻¹(x) ���قȂ�2�_�Ō����v�Ɓuy��f⁻¹(x)��y��x ���قȂ�Q�_�Ō����v�����l�ł���Ƃ����L�q�����������̂ł����A
A=B����������
>>799 P=(f��f⁻¹���قȂ�2�ȏ�̓_�Ō����)
Q=(f⁻¹��y��x ���قȂ�2�ȏ�̓_�Ō����)
R=(f�͘A��)
S=(f��f⁻¹��y��x ��ɈقȂ�2�ȏ�̋��L�_������)
�Ƃ��āA�咣�́u�C�ӂ�f�ɂ���(P��Q)��(S����R)�v�Ɠǂ߂��ł��������Ă܂����H
>>768 762�ł�
������菕����A���肪�Ƃ�
��[0 to a] exp(-x^2) dx =I[a]�Ƃ��A
>>803 ��.��.��.��.��.��..�K�C.�W.
�a.�@.��.�s.��.��.��.�K.�C.�W
>>803 �����ϕ��ɂ��
��exp(-xx) dx = -(1/2x)exp(-xx) - ��(1/2xx)exp(-xx) dx
�@= -(1/2x)exp(-xx) + {1/(4x^3)}exp(-xx) + ��{3/(4x^4)}exp(-xx) dx
�@= ����
���@I[a] = I - [1/(2a) - 1/(4a^3) + 3/(8a^5) - ����] exp(-aa)}
t = 0.87752700406522
n = 0,
����a[n]=1/n�̊e���ɑ��Ĉȉ��̑���(T)���s���A�V���Ȑ���b[n]�����B
>>808 �|�G���ł͂Ȃ������肷����@��������܂���
>>807 b[n] �̏����_��m�ʈȊO�̈ʂ�S��0�ɂ������� b_m[n] �Ƃ����A
lim_(m����) ��_(n=1,��) b_m[n]
= lim_(m����) ��_(n=1,10^m) b_m[n]
= lim_(m����) (10^(-m))*��_(k=1,(10^m)/2) ��_( 1/(2k+1)��n/(10^m)<1/(2k) ) ((2k)mod10)
= ��_(k=1,��) ((2k)mod10)/(2k(2k+1))
= ��_(0,1) (2x^2+4x^4+6x^6+8x^8)(1-x)/(1-x^10) dx
�� 0.652562.
���̒l�� �� �Ƃ����� ��_m := ��_(n=1,10^m) b_m[n] �� lim_(m����) ��_m = �� �����̂�
lim_(m����) ��_(n=1,m) (��_n)/m = ��.
����炩��A���̐��� n �ɑ��� 10^m��n<10^(m+1) ��������k���Ƃ��
��_(k=1,n) b[k]
= 1 + ��_(k=1,n) ��_(j=1,��) b_j[k]
= 1 + (��_(j=1,m-1) ��_j) + ��_(j=m,��) ��_(k=1,n) b_j[k]
= 1 + (1+o(1))m�� + ��_(j=m,��) (��_j)*8n/(10^j)
(�������e j �ɑ��� ��_j �� 0 �ȏ� 1 �ȉ��̎���)
= 1 + (1+o(1))m�� + 72��n/(10^(m+1))
(�� �� 0 �ȏ� 1 �ȉ��̎���)
= (1+o(1))��logn.
����āA�Ɍ��l�͑��݁B���łɂ��̋Ɍ��l�̓�.
>>803 (��/4)I = 0.7854�EI < 0.8427�EI = erf(1)�EI = I(1) =��[0,1] exp(-xx) dx,
���ӂ� ��[0,t] exp(-xx) dx �Ƃ���ƁA
t < 1,
n = 0.
>>810 �����
��
> = ��_(0,1) (2x^2+4x^4+6x^6+8x^8)(1-x)/(1-x^10) dx
> �� 0.652562.
��
= ��_(0,1) (2x+4x^3+6x^5+8x^7)(1-x)/(1-x^10) dx
�� 0.956876.
��
> = (1+o(1))��logn.
> ����āA�Ɍ��l�͑��݁B���łɂ��̋Ɍ��l�̓�.
��
= (1+o(1))��log_10(n).
����āA�Ɍ��l�͑��݁B���łɂ��̋Ɍ��l�̓�/ln10. ������ln�͎��R�ΐ��B
>>793 C{k-1,2} = C{k,3} - C{k-1,3}
&
C{2,3} = 0,
>>780 http://poemehonpo.co.jp/ �@�{�܁@�����s�������T
http://www.poeme.co.jp/ �@���R�X���Ɨ������B�@�����s���V���b
>>807 >>812 (��)
(1-x^10)/(1-x) = 1+x+x^2+����+x^9
�@= (1+x)(1+x^2+x^4+x^6+x^8)
�@= (1+x)(1-x+x^2-x^3+x^4)(1+x+x^2+x^3+x^4),
���
(2x+4x^3+6x^5+8x^7)(1-x)/(1-x^10)
= (2x+4x^3+6x^5+8x^7)/{(1+x^2+x^4+x^6+x^8)(1+x)}
= (4-2x+6x^2-2x^3+6x^4+4x^6+4x^7)/(1+x^2+x^4+x^6+x^8) - 4/(1+x)
= (4-3x+6x^2-4x^3+6x^4-3x^5+4x^6)/(1+x^2+x^4+x-6+x-8)
�@+ (x+2x^3+3x^5+4x^7)/(1+x^2+x^4+x^6+x^8) + F(x)
= (3xx-4x+3)/2(1-x+x^2-x^3+x^4) + 5(1+xx)/(1+x+x^2+x^3+x^4) + E(x) + F(x)
= (�Ӄ�/2)/(xx-��x+1) + {1/(2�Ӄ�)}/(xx+x/��+1) + (1+��/2)/(xx+��x+1)
+ {(3-��)/2}/(xx-x/��+1) + E(x) + F(x)
= A(x) + B(x) + C(x)+ D(x) + E(x) + F(x),
�� A(x) dx = {(�Ӄ�-2)/�Ӂ�(4-�Ӄ�)}arctan{(2x-��)/��(4-�Ӄ�)},
�� B(x) dx = {(2+��5)/��(5+2��5)}arctan{(2��x+1)/��(4�Ӄ�-1)},
�� C(x) dx = (��/2)��{2(5+��5)}arctan{(2x+��)/��(4-�Ӄ�)},
�� D(x) dx = {(2+��)/�Ӂ�(4�Ӄ�-1)}arctan{(2��x-1)/��(4�Ӄ�-1)},
�� E(x) dx = (1/2)log(1+x^2+x^4+x^6+x^8) = (1/2)log{(1-x+x^2-x^3+x^4)(1+x+x^2+x^3+x^4)},
�� F(x) dx = -��4/(1+x) dx = -4log(1+x),
���̒���
���@�܂�
>>807 �悭������ A[n]/B[n] �̋Ɍ�������c
>>812 �ŋ��߂��̂͋t�� B[n]/A[n] �̋Ɍ��l�ł��邱�Ƃɒ��ӁB
>>817 �����I�ɕ\�����c���������C
�����Ŕ��Ώ̗������藧�ĂT�C�N�����������Ė{�ɏ����Ă������
���̖{�͌������ƂȂ����ǁA�^�ɈقȂ�2���ɂ��Ă̘b����Ȃ��́H
0<1<2<...<n-1�Ə����t���R��ꂽ{1,...n-1}��n�v�f�̑S�����Ɠ��^�Ƃ�
�ӂ̒�����a,b,c(0<a<b<c�Aa^2+b^2+c^2=1)�̒����̂��A�Ίp�������Ƃ��ĉ�]�������Ƃ��ɒʉ߂��镔���̑̐ς����߂�B
������Ȃ���ł���
����v���܂��B
K��1�̌��nn�捪�Ă��܂ނƂ��A����g��L/K�͙p���g��ł���B�ƁA�K���A���_�̖{�ɁA�����Ă����ł����A������ăq���x���g�̑�12���̓���ȏꍇ�ł����H
���݂܂���B������Ȃ����X���ɏ������Ƃł͂Ȃ������ł��ˁB����X���s���Ă��܂��B
>>827 0�����x�N�g����Ԃ̊��̓ӂƂ������킯�킩��Ȃ����̂���Ȃ��͂��ł���
�����Ɛg�߂Ȃ��̂Ȃ͂��ł���
n,p,q,r�͐�����p+q+r=n����
>>831 �����A0����vector��Ԃ̊��͋�W��∅�ł��B
�Ƃ������A����1�_����Ȃ���Ȃ̂�
>>832 �����܂���A�����ł͂Ȃ����R���ōl���Ă�������
>>833 1�_������Ȃ��W���ł͂Ȃ��ł����
����1�_�Ƃ͋�̓I�ɂ͂Ȃ�ł����H
>>831 ���݂܂���B�r���ő��M���Ă��܂��܂����B
����1�_����Ȃ�K-vector���V={0}�̊��͋�W��∅��������܂���̂ŁA
dim(V)=|∅|=0 �Ƃ����̂��������ł��B
�Ȃ��A����̓��e�ɂ��ẮA
���ȉ������܂����B
���������肪�Ƃ��������܂����B
>>835 ���Ȃ��Ă���r���ɑ��M���Ă��܂��܂����̂ŁA
�u����1�_����Ȃ���v�Ƃ����Ӑ}���Ȃ����͂𑗂��Ă��܂��܂����B
����v���܂����B
�O
>>797 >>824 xyz��Ԃɓ_(a,b,c)��a��b��c�ƂȂ�悤�ɂƂ�A�_(0,0,0)�ƌ�������Ίp���Ƃ��钼���̂����̒��������Ɉ��]������ƁA�����̂̒ʉߕ����́A
�~���Ɖ~������Ăꂱ�ɂ��ĉ~����̂����������̒�ʂŒ��肠�킹���ۂ̂悤�Ȍ`�B
�_(0,0,0)���_(a,b,c)�����Ɠ݊p�ɂƂ��������_�B
�I���I������V�n�Ώ̂ɂ����`�B
�����̂�z���ɕ��s�ɓ������f�ʂ��A�cc����(a^2+b^2)�̒����`�ŕ`���ƁA�Ίp���̒����͑�ӂ��A
��(a^2+b^2+c^2)=1
���p�O�p�`�̍����ƃs�^�S���X�̒藝���A�~������щ~����̔��a�ƍ�������肷��B3�ӂ̔�͂��������ق�����A
1:c:��(a^2+b^2)
=1:c:��(1-c^2)
�~��=(1/3)��{c^2/(1-c^2)}(1-c^2)
=��c^2/3
�ی`���̂̍ő唼�a
=c/��(1-c^2)
�Ίp�������̒�ʐ�(�ی`���̂̂��т�Ă镔���̍ŏ��f��)
=(1/2){c/��(1-c^2)}(1/c^2)
=1/2c��(1-c^2)
�~����=(1/3)��{c^2/(1-c^2)}-(1/3)��{1/4c^2(1-c^2)}(1/2)
�������̂̒ʉߕ����̑̐�
=2(�~��+�~����)
=2��c^2/3
+2(1/3)��{c^2/(1-c^2)}-2(1/3)��{1/4c^2(1-c^2)}(1/2)
=2��c^2/(1-c^2)-��/12c^2(1-c^2)
=(8c^2-1)��/12c^2(1-c^2)
>>839 ���肪�Ƃ��������܂�
�ł�c=1/��3�Ƃ��Ă�������v���܂���
>>837 ����ꎟ�Ɨ�����Ȃ��ł����
�O
>>839 >>840 a��b��c������A
c=1/��3�Ɖ��肵����Aa��b�����݂��Ȃ����낤�B
a^2+b^2=1-c^2=1-1/3=2/3
a��b��c���Z���B�܂�c�́A
1/��3��c
1/��3��肨�������͂��ŁA���̉���ɖ�������B
�R�����~���Ƃ��̑g�ݍ��킹�ɂ͂Ȃ�Ȃ���Őϕ����Ȃ��Ɩ�������H
>>842 <�ł͂Ȃ�<=�ł����\����Ȃ��ł���
a=b=c�̂Ƃ��̓�/9�ɂȂ�͂��Ȃ�ł�
>>843 �����ł��ˁA�~��2�Ɖ�]��t�o�ȖʂƂ���2�̕��̂ɂȂ�͂��ł�
>>832 �W��
nCr = (n!)/((n-r)!)(r!)
�������ł��邱�Ƃ��g���A���̐ςŕ\���B
(p+q+r)!/(p!)(q!)(r!)
= (p+q)!/(p!)(q!)�E(p+q+r)!/((p+q)!)(r!)
= (p+q)Cq�E(p+q+r)Cr
2�̓W���͐���������A�^���͐����B
�O>>842 >>844 >>843 �̐�1�̒����̂�Ίp�������Ɉ��]������ƁA�Ίp���ɑ��Ă˂���̈ʒu�ɂ��钷��c�̒��ӂ��ʉ߂��镔���͂Ȃ߂炩�ȋȖʂɂȂ�ˁB �O
>>846 �ە������C�B
xyz��Ԃɓ_(a,b,c)��a��b��c�ƂȂ�悤�ɂƂ�A�_(0,0,0)�ƌ�������Ίp���Ƃ��钼���̂����̒��������Ɉ��]������ƁA�����̂̒ʉߕ����́A
���ʂ��o�Ȗʂ̌ۂ̗��ʂɉ~�����Ăꂱ�ɂ��Ē�ʂ肠�킹���`�B
�_(0,0,0)���_(a,b,c)�����Ɠ݊p�ɂƂ��������_�B
�I���I������V�n�Ώ̂ɂ��đ��ʂ��Ȃ߂炩�ɂ����`�B
�����̂�Ίp����z�����Ȃ����ʂœ������f�ʂ��A�cc����(a^2+b^2)�̒����`�ŕ`���ƁA�Ίp���̒����͑�ӂ��A
��(a^2+b^2+c^2)=1
���p�O�p�`��3�ӂ̔�͂��������ق�����A
1:c:��(a^2+b^2)
=1:c:��(1-c^2)
�~��=(1/3)��{c^2/(1-c^2)}(1-c^2)
=��c^2/3
�ی`���̂̍ő唼�a
=c/��(1-c^2)
���p�O�p�`�̍����ƃs�^�S���X�̒藝���A
�~���̒�ʂ̔��a�́A
c/��(1-c^2)
�~���̍����́A
1-c^2
�o�Ȗʂ̍����́A
1-2(1-c^2)=2c^2-1
�o�ȖʊԂ̉~�Ղ̔��a���ۂ̒�ʂ���̋���t(0��t��c^2-1/2)�ŕ\���ƁA
�ϕ�����B
�������̂̒ʉߕ����̑̐�
=2(�~��+���ʂ��o�Ȗʂ̉~��)
=2��c^2/3
+2��[t=0��c^2-1/2](�o�ȖʂƑΊp���̋���)^2dt
=
�o�ȖʂƑΊp���̋������Ȃ킿�o�Ȑ��ƒ����̋�����t�̊��ŕ\����ΐϕ������킩��͂��B
�O
>>847 �����̔���8�̒��_�̂���������2�̒��_��e�w�ƒ��w����w���炢�ŋ��ނ悤�Ɏx���A�Ίp�������ɔ����͂����A�������ʼn�]�����Â���ƒʉߕ������킩��B
�ł���\�t�g�^�C�v���{�b�N�X�^�C�v�������B���J���ł���Ȃ��悢�B
�Ώ̎��ɑ��锼�a�̋ɑ�l�͏�3�A��3�B�w���G��ĂȂ�6�̒��_�̂��ꂼ��ɂ���B
���a�̋ɑ�l�͏ォ��A
a��(b^2+c^2)=a��(1-a^2)�\�\�@
b��(c^2+a^2)=b��(1-b^2)�\�\�A
c��(a^2+b^2)=c��(1-c^2)�\�\�B
c��(a^2+b^2)=c��(1-c^2)�\�\�C
b��(c^2+a^2)=b��(1-b^2)�\�\�D
a��(b^2+c^2)=a��(1-a^2)�\�\�E
�����̔��̏ꍇ�A
a��b����(a^2+b^2)��c����(c^2+a^2)����(b^2+c^2)
�����A��(a^2+b^2)��c�̑召�W�͌��܂��ĂȂ��B
�召���ς��·A�`�D�͏��Ԃ�����ւ��B
������12�{����ӂ̂����w���G��ĂȂ�6�{�̕ӂ͂˂���̈ʒu�ɂ���B
��]���ƂȂ�Ίp���ɑ��Ă˂���̈ʒu�ɂ���6�{�̕ӂ��`���O�Ղ͑o�ȖʁB
�w���G��Ă�6�{�̕ӂƂ��̓������`���O�Ղ͉~���ŏ㉺���킹��12�B
>>845 �}���قœǂ��ϕ��̖{�ŁA
>>851 �ǂ�
���f�ϕ������K�ł��邱�Ƃ��l�����ĂȂ��{�ɂ����Ȃ�o�ꂵ�����ď���������
>>852 �ϕ��͖ʐς��Ȃ����Ă�悤�ȃA�z��
����()�Ȃ�čl�����Ƃ���ňӖ���������
����������ƍL�����E�̕������Ă���߂��Ă����ł�
�����m��Ȃ��A�z����X���߂Ȃ�Ă��Ă������Ƃ����
���̈Ӗ��������ǂ��납�A�p���ĊQ�ɂ����Ȃ�Ƃ����������
>>853 ���Z���̐ϕ��Ȃ�āA�敪���ς���ϕ��̊�{�藝�ŊȒP�Ɍv�Z�ł��܂��A���x�ł����Ȃ�
���������Z���Ƃ��Đ������̍H�w���������̐������Ȃ��ϕ���Ԃ�i�����Ă鐔��������A�˘f���͓̂��R�Ǝv��Ȃ��H
���łɁA���̎Q�l�����Ă��ǂ��ɂ��ϕ���Ԃ�i����Ă��������ڂ��ĂȂ�������
>>850 �ӂށB�w��ł��Ȃ����Ƃ�O��Ƃ��Ă���̂ł���A���Z������ɗ��Z�Ō��Z�̈��i�����������Ȃ̂��낤�B
�܂�A�l���Ă���\���L���̈�Ő����ł��邱�Ƃ����炩�Ȃ悤�Ȋ��������l���Đ������Ă���̂��낤�B
f(x) �̌��n���� F(x)�@�Ƃ���Ƃ�
F(ki)-F(0)�@�Ő������l���^�����锤�B(�ϕ��o�H�͖��ɂȂ�Ȃ����Ȃ̂�)
>>807 ��`�����m�łȂ�
0.5��10�i�\�L�ɂ�0.49999999999�c������
https://imgur.com/cooKcRK (1) ���̘A���������̉��������������߂�B���̎��̉������߂�B
3x+4y+5z = a
2x+3y+4z = b
x+2y+3z = c
(2)���̊�f(x)��x=1/2�𒆐S�Ƀe�C���[�W�J����B���̎��̎������a�����߂�B
f(x) = 1/(x^2-x+1)
����2�肪�����Ȃ���ł����A�ǂ������炢���ł��傤���E�E�E�H
�����I�ɂ���Ă݂���ł����A(1)��rankA = rankAb�@�ɂȂ�Ȃ��Ɖ�����ɋ��܂�Ȃ�����Az��K���Ɍ��߂Ă�����H�Ƃ��������œZ�߂܂����B
(2)�Ɋւ��ẮA�Ƃ肠������K�������Ă݂���ł����A�������Ⴄ�����o���̂Œ��߂܂����B�B�B�B
>>854 �H�w�����Ȃ瓹��Ƃ��Ďg�����������������
�P�X�A�˘f���K�v����
����������܂���Ă����ŏ\�����낤
�H�w�������̗������ڂꂪ�����ɍl���Ă��d���˂������
�����Ă��Ăǂ����Ă��m�肽�����Ƃ�����Ȃ�
�����Ȗ{�ɓ���������A���ׂ�͕̂��ʂ̎�
���ꂪ�ł��Ȃ����痎�����ڂꂽ�̂ł�
>>656 (1)���Ƃ��Ɖ�����ӂɒ�܂�͂��Ȃ��B
�����v0���Ƃ߂āAAv=0�̔���v1���߂�v=v0+kv1
(2)������������
�}�X�^�[�I�u�����̌������ł��B
����̇A���������R��������܂���B
�e���̐����̍���3�Ƃ��čl���Ă���̂Ȃ�A2-9��3�������悤�ȂƂ��ɑΉ����Ă��Ȃ��Ǝv���̂ł����B
��낵�����肢���܂��B
>>861 ���A������܂����B�J�艺���̂Ƃ�+10-1���čl���邯��mod�ōl���邩��W�Ȃ��̂ł��ˁB
>>858 rank((3, 4, 5), (2, 3, 4), (1, 2, 3)) = 2
�Ȃ̂ŁA���̕������͎�����
px + qy + rz = s
tx + uy + vz = w
�i1����2�{�̕������j�Ɠ����B
�܂�A3�{�ڂ̎�������2�{�̎���
�������Ȃ���悢�B
x + y + z = a - b = b - c �ł��邩��A
a + c = 2b�ia, b, c �����̏��ɓ�������j
�ł��邱�Ƃ��A���������߂̕K�v�\�������B
>>858 �i���j
x + y + z = a - b = b - c = d �Ƃ�����
a = c + 2d�Ab = c + d
�܂� -x + z = c - 2d�Ay + 2z = c - d �Ȃ̂ŁA
x = z - c + 2d�Ay = -2z + c - d
�Y��ɂ��邽�߂� z = t + c - d �Ƃ����A
(x, y, z)
= (t + d, -2t - c + d, t + c - d)
= (
>>858 x^2 - x + 1 = (x - 1/2)^2 + 3/4 �ł��邩��A
t = (x - 1/2)^2�Aa = 3/4 �Ƃ����āA
t = 0 �ł� Taylor �W�J������悢�B
f(x) = 1/(t + a)
= (1/a)(1/(1 + u)) �iu = t/a �Ƃ������j
= (1/a)(1 - u + u^2 - u^3 + �c�c)
= (4/3) �[k=0, ��] (-1)^k (x - 1/2)^(2k)
>>858 �x�N�g��(1,1,1)��n�Ƃ��āAn�ɐ����ȕ���x+y+z=t��V����(����)xy���ʂ̂悤�ɍl�������̋�Ԃ̊��x�N�g���̂���(1,1,1)�ȊO�̂��̂����߂����̂ł����A�ǂ������炢���ł��傤���H
�K��ɂ��@(1,-1,0)/��2�@(1,1,-2)/��6�@�Ƃ���B
>>861 �U�D�@7�A4281�C071 �� 99 �Ŋ��肫���悤�ɁA1�����̐� (�A)�A(�C) �����߂�B
�@7042810071 + (10^8)(�A) + 1000(�C) �� 66 + (�A) + 10(�C)�@(mod 99)
�@(�A) = 3,�@(�C) = 3,�@7342813071 / 99 = 74169829.
�V�D�@1998�̔{���̂����A�e�ʂ̐������ׂē������ŏ��̐������߂�B
�@1998 = 2(10^3 -1),
�@333667 = (10^6 +10^3 +1)/3,
�@�ӁX�|���� 6 (10^9 -1)/9.
>>868 ���݂܂���A�ǂ̂悤�ɋ��߂������m�肽���ł�
>>863 >>864 >>865 >>866 �����J�ɂ��肪�Ƃ��������܂��B��ς�������܂����B���肪�Ƃ��������܂��I
>>870 �K��ɂ��A�݂��ɐ����ɂȂ�悤�ɂ���B
�O�����E�V���~�b�g�̐��K�������@
>>869 ��̖��܂ʼn��肪�Ƃ��������܂��I
333667 = (10^6 +10^3 +1)/3
����͂ǂ̂悤�ɂ��Ĕ�������̂ł����H
>>869 ���x�����݂܂���B
333667 = (10^6 +10^3 +1)/3����͂������Ă����̂ł����B
�X�ɋ^�₪�A�ŏ�����(10^6 +10^3 +1)/9�A(10^3 +1)/3�A (10^3 +1)/9�A(10^3 +1)/2�����ꂼ�ꐮ���łȂ����Ƃ������Ώ\���Ȃ̂ł����H
�O
>>848 >>824 �����̔���Ώ̎����Œ��ɂȂ�悤�Ɏ����A���]������ƁA�㉺�Ώ̂ȉ~��2�Ɖ~����10��ςݏd�˂����̂ɂȂ�B
��]���ł���Ίp���Ƃ˂���̈ʒu�ɂ��锠�̍Œ��ӂ���肾���o�ȖʂƑΊp���̍ŏ�������1/2�Ȃ�A�o�Ȗʂ͉~����̓����B
�ʉߕ����͉~���Ɖ~����̂݁B
���Ȃ�M�U�M�U�ȎO�A�����ƂȂ�B
�Ώ̎�0�`1�̂����A
0�`a^2�\�\�@�͉~���A
a^2�`a��(1-b^2)/{ab+��(1-a^2)(1-b^2)}�\�\�A,
a��(1-b^2)/{ab+��(1-a^2)(1-b^2)}�`b^2�\�\�B,
b^2�`b��(1-c^2)/bc+��(1-b^2)(1-c^2)�\�\�C,
b��(1-c^2)/bc+��(1-b^2)(1-c^2)�`c^2�\�\�D,
c^2�`1/2�\�\�E��5�敪�͉~����5�A
1/2�`1-a^2��5�敪���~����5�A
1-a^2�`1�͉~���B
�~��2�Ɖ~����10�̘a�́A�~��1�Ɖ~����5�̘a��2�{�B
�@(1/3)��a^2(1-a)^2a^2
=��a^4(1-a^2)/3
�A��/3a^2-��a^(1-b^2)[1-a(1-b^2)/{ab^2+b��(1-a^2)(1-b^2)]/3{ab+��(1-a^2)(1-b^2)}^2
�B��b^4(1-b^2)/3-��a^3(1-b^2)^2/{ab^2+b��(1-a^2)(1-b^2)}/3{ab+��(1-a^2)(1-b^2)}^2
�C��/3b^2-��b^(1-c^2)[1-b(1-c^2)/{bc^2+c��(1-b^2)(1-c^2)]/3{bc+��(1-b^2)(1-c^2)}^2
�D��c^4(1-c^2)/3-��b^3(1-c^2)^2/{bc^2+c��(1-b^2)(1-c^2)}/3{bc+��(1-b^2)(1-c^2)}^2
�E��{8c^2(1-c^2)^2-1}/24
�ʉߕ����̑̐�=2(�@+�A+�B+�C+�D+�E)
=2��a^4(1-a^2)/3
+2��/3a^2-��a^(1-b^2)[1-a(1-b^2)/{ab^2+b��(1-a^2)(1-b^2)]/3{ab+��(1-a^2)(1-b^2)}^2
+2��b^4(1-b^2)/3-��a^3(1-b^2)^2/{ab^2+b��(1-a^2)(1-b^2)}/3{ab+��(1-a^2)(1-b^2)}^2
+2��/3b^2-��b^(1-c^2)[1-b(1-c^2)/{bc^2+c��(1-b^2)(1-c^2)]/3{bc+��(1-b^2)(1-c^2)}^2
+2��c^4(1-c^2)/3-��b^3(1-c^2)^2/{bc^2+c��(1-b^2)(1-c^2)}/3{bc+��(1-b^2)(1-c^2)}^2
��{8c^2(1-c^2)^2-1}/12
�O
>>875 �ŏI�s�A�̑O��+���������B
>>824 �����Ă�Ǝv���B
a^2+b^2+c^2=1���g���ĕ�����3��������2�����Ɍ��炷���Ƃ͉\�����A�^����ꂽa,b,c�������ɉe�����邱�Ƃ��v���A3�Ƃ��g���Ă����Ǝv���܂��B
���������ȒP�ɂȂ�\���͂���B
>>874 ���Z���w�̔��������������
>>876 ���肪�Ƃ��������܂�
��������ǂ�ŗ����������Ǝv���܂�
x,y�ɂ��Ă̘A��������
>>879 ���Z���w�̔��������������
>>879 ���ꍂ�Z��.�w��.��.��.��.��.��.�ɏ����Ă܂���
�Y�z�C�ł��鐹��͈�ʕ����ł��邱�Ƃ�����
�₽��Ɩ{���`���Ă�z�������
>>879 s=0, t=1 �̂Ƃ��@�c�@���Ȃ��B
����ȊO�̂Ƃ�
�@x = {a(1-t)+s}/{ss+(1-t)^2},
�@y = {as-(1-t)}/{ss+(1-t)^2},
(1) a=0 �̂Ƃ�
�@|x+2y| = |s-2(1-t)|/{ss+(1-s)^2},
�@s=2(1-t), 0<s��1, 1/2��t<1�@�̂Ƃ��ŏ��l�@0
>>879 ���`�㐔���ۂ��]���A >>886 ���̖��������̐������_�����ے肳���̂��H
�u���n����B�v�ƕ������Ă������A�������_�������W�F�N�g���ꂽ����ƌ�����
���������������Ȃ����͗D�G�Ȑ��w�҂͔��f�\���낤����A�������̊Ԃɂ�
���₳���Ă��������Ba�Ab�Ac�Ad��4�`�[�����N�W�������ăg�[�i�����g�Ŏ���������ꍇ�Aa��B��1���őΐ킷��m����3����1�H2����1�H�ǂ����ł����H
>>893 ���N�U
a��B�Ƃ����g�������Ȃ�h�A�z
���₳���Ă��������Ba�Ab�Ac�Ad��4�`�[�����N�W�������ăg�[�i�����g�Ŏ���������ꍇ�Aa��b��1���őΐ킷��m����3����1�H2����1�H�ǂ����ł����H
>>895 ���Z���w�̔���������ɏ����Ă�B
72/129
>>896 ����ȉ��ɏ�����ł�������A�ǂ�����������^�R
>>895 �Ӗ��s���ȋt�����������A�������Ȃ��������̂悤�ɖ��`�F���W
���O�G������
>>895 �t�ɂǂ��l������1/2�Ǝv����̂��m�肽���Ƃ���
�g�[�i�����g�\�����Ă݂������������̂�
�ꎎ���ŏ\�{�̃z�[���������o���`�[����
�O
>>876 >>901 �z�[��������ł��ăz�[���x�[�X�܂Ȃ������I�肪�A�E�g�ɂȂ邱�Ƃ��������B
�����I��͈�ۃx�[�X�ݖY��ăs�b�`���[�S���ɂȂ����B
���ŏ����̓_����0�_
A,B��2�������s��ł���A
>>903 �N������K�v�Ƃ���Ȃ����������ǂ̃L�`�K�C
���݂܂���ʂ��ԈႦ�܂���
�|�G�}�[�́@�ʂ��ԈႦ�̂��������@���ڂ����I
�S�~�͖ϑz�̓d�g����o����̂���߂Ă���A���ɏ�i�������̂�10�N�ȏ�O��
�E�܂ł�����ł���̂�߂ĂˁA���ʏՓ˂Ŏ��E�������̂�������Ȃ���
�e���r�œd�g����o����A�z�͔r���ł��Ȃ��́H
>>907-909 �͕�����Ȃ����Ƃ������Ă���
���w�W�Ȃ����A�����̃X���ŕ����Ă�
�O
>>902 >>913 �������Ă��ꂵ���ł��B���肪�Ƃ��B
�싅�̃��[���ɂ͏ڂ����Ȃ��̂����A
���͂␔�w�̃X������Ȃ���Ȃ���w
���₢��A
>>901 �̖��L�q��
>>902 �𐳉��Ƃ���.
>>913 �ւ̋^�`�䂦�A�܂��܂����̐��w�̃X���̂����B
>>902 ,917����~������ɁA�ŋ����t�F�A�̈����Ă̂܂܊ϋq�Ȃɗ��������ꍇ�A
�Ŏ҂��S�ۂ�Ńz�[���ɓ��B�����ꍇ�̂݃z�[�������Ƃ��ē��_���Z�B
����ȊO�̏ꍇ�́A�L�^��͓��ۂ܂ł̗ۑłŁA���_�͖���(�܂�z�[�������ł͂Ȃ��j
�̂ɁA
>>901 �ւ̓��́A���L�q�Ńz�[�������Ƃ��Ă���ȏ�S�ۂ�ł��邱�ƂɂȂ�̂ōŏ����_��10�A�Ƃ������ƂɂȂ�ȁB
AB+BA=E
�L�������̃x�N�g����Ԃ��^����ꂽ�Ƃ��A���̑S�Ă̊��������邱�Ƃ͂ł��܂����H
�����邱�Ƃ��ł���A�Ƃ͂ǂ��������Ƃł����H
>>920 N�����̉^���̉e��M����(M<N)�ɓ��e�����ꍇ�A
1�s�ڂ����Ȃ̂ł����A���̉��Ă��������_������Ǝv���܂����H
�Δ����Ȃǂ悭�������Ă��Ȃ��̂Ŏ��M�����ĂȂ��̂ł���
>>927 �����܂���グ�����ł�
>>928 �����F�߂Ă��炦�Ȃ��ł��傤�B
�����ϐ��݂̂����Ďc��̕ϐ����Œ肵�čl�����Ƃ��ɂ���_�ōŏ��ƂȂ邱�Ƃ́A�S�Ă̕ϐ������R�ɑS�����������Ƃ��A���̓_�ōŏ��ƂȂ鎖�̕K�v�����ł͂���܂����A�\�����͊m�F���Ȃ��Ǝ����Ƃ͔F�߂Ă��炦�Ȃ��Ǝv���܂��B
>>929 ���̕��j�ł�肽���Ȃ�
x�̑S�Ă̒l���������Ȃ��ꍇ�A�������Ȃ�2������ĕ��ς���蓙��������ƁAF�͂�菬�����Ȃ�
������J��Ԃ���x���S�ē������Ȃ�
���ꂪ�����Ȃ��ƃ_�����Ă��Ƃł��ˁB���肪�Ƃ��������܂�
�����������̑���J��Ԃ��Ɠ������Ȃ邩������Ȃ�Ȃ��ł�����˂���c
3����x�Ȃ����l����ƁA�S�Ă��������Ȃ�Ō�̑���̒��O�A���ς���̃Y����0,��,-���ɂȂ��ĂȂ��Ƃ����Ȃ�����
�����z�u�����ꂶ��Ȃ��Ɩ������Ă��Ƃł������
���肪�Ƃ��������܂���
KL�����̓��o�͍H�w��1�N�Ƃ��ĕK�{�ł����H
�������̉���a,b�Ƃ����Ƃ�
>>920 >>934 4�����ōl�����牽�������邩�������
>>920 >>936 ���肪�Ƃ��������܂�
�l�����Ƃ͎l���������Ƃ������Ƃł��傤��
���������Ȃ�l���������ɂȂ���[���b�Ƃ������Ƃł����H
>>928 �Ǝv�������ǁA�u�S�Ă�x���������Ȃ�����A���F�͍ő�łȂ��v�Ƃ������Ƃ͂��ꂩ�猾����͂��Ȃ̂ŁA����������ok�ł��傤���H
�ԈႦ��xa+xb=k-S�Ə����Ă��܂��Ă܂����Axa+xb=S�ɓǂݑւ��ĉ������B
�������c�c�u�ŏ��łȂ��v�ł����݂܂���
>>931 ���w�I�A�[�@��
��[i=1,j-1](x_i*ln(x_i))����[i=1,j-1](x_i)*ln(��[i=1,j-1](x_i)/(j-1))
�˃�[i=1,j](x_i*ln(x_i))����[i=1,j](x_i)*ln(��[i=1,j](x_i)/j)
�������Ȃ����ȁH
�����
��[i=1,n](x_i*ln(x_i))����[i=1,n](x_i)*ln(��[i=1,n](x_i)/n)=k*ln(k/n)
��������A��[i=1,n](x_i)=k�ƂȂ�C�ӂ�{x_i��0}�̑g�Ō����邯���
>>940 >
>>928 > �Ǝv�������ǁA�u�S�Ă�x���������Ȃ�����A���F�͍ő�łȂ��v�Ƃ������Ƃ͂��ꂩ�猾����͂��Ȃ̂ŁA����������ok�ł��傤���H
F�ɋɏ��l�����邱�ƂƁA�S�Ă�x���������Ȃ���F��菬����F'�����݂��邱�Ƃ�
�����邯��ǁA
F'���ɏ��l��菬�����\����ے�ł��Ȃ�
Lie�Q�̕��Ք핢�Q���܂�Lie�Q�ƂȂ邱�Ƃ͂ǂ̂悤�Ɏ�������ǂ��ł����H
>>928 n��2,
�@x_i �𐳂̐��Ƃ��A��[i=1,n] x_i = k�@���݂����Ƃ���B
��[i=1,n] (x_i)^(x_i) �̍ŏ��l�����߂�B
(����)
�@log(x) - log(k/n) = - log(k/(nx)) �� - {k/(nx) -1},
�@x log(x) - x log(k/n) �� x - k/n,
i=1�`n �ł����B
�@��[i=1,n] (x_i)log(x_i) - k log(k/n) �� k - k = 0,
�@��[i=1,n] (x^i)^(x^i) �� (k/n)^k,
�����ׂĂ� {x_i} �����R�ɓ������Ă��A���ꂪ�ŏ��l�B
���邢��
�@f(x) = x log(x)�@�Ƃ����Ɓ@f "(x) = 1/x >0�@(���ɓʁj
�@Jensen �ť���
>>943 �A�z�ł����܂���c�c����Ă悭�킩��܂���
�@�Ⴄ2��x���܂ގ��͐�ɍŏ��łȂ�
�A�Ⴄ2��x���܂܂Ȃ�x�̑g�͑S�Ă�������1�g�����Ȃ�
�B�Ȃ̂ōŏ��̌��͂��ꂵ���Ȃ��A����Ă��ꂪ�ŏ�
������Ę_���Ƃ��Ă���ς�ア�ł����H�����ĂĂ����M�����ł���
>>942 �͔͉ł�xlogx����ɓʂȂ��Ƃ𗘗p���ċA�[�@�Ŏ����Ă��܂����Bjensen�s�����ƌ�������Ǝv���܂�
>>945 ���肪�Ƃ��������܂��B
���̐��ɑ���logx��1-(1/x)�Ȃ̂ł��ˁB����m��܂���ł����c
����[����͂��ꂢ�ȉ������ł��ˁB���肪�Ƃ��������܂��B
���ځA������Ȃ����ǖ��ł͂Ȃ���ł����c
>>924 �S�ėł��邩�Ƃ������Ƃł�
>>950 ����Ȃ���Ȃ�ł����c�B
���߂�10�ʂ͖�������Ȃ̂ł����ˁH
����n�̊���ڂ̐����̍��v��A[n]�A�������ڂ̐����̍��v��B[n]�Ƃ����B
���w�̍ō���100�Ȃ獂�Z���w��2�Ƃ�3���낤��
>>955 ����Ȃɂ���H�B
ABC���_�̉����_����100�Ȃ�A7������H
>>946 > �@�Ⴄ2��x���܂ގ��͐�ɍŏ��łȂ�
> �A�Ⴄ2��x���܂܂Ȃ�x�̑g�͑S�Ă�������1�g�����Ȃ�
> �B�Ȃ̂ōŏ��̌��͂��ꂵ���Ȃ��A����Ă��ꂪ�ŏ�
> �B�Ȃ̂ōŏ��̌��͂��ꂵ���Ȃ�
����́A�ŏ������݂���Ƃ����炱��ł���A�Ƃ������Ƃ������Ă��邾���ŁA�ŏ��l�����݂��Ȃ��ꍇ��ے�ł��Ȃ�
�Ⴆ��-���܂ł�����ł��������l���Ƃ��ꍇ��A
�A�̋ɏ��l��菬���������������Ƃ��āA������ł��߂����ɒl���Ƃ�邪�A���̒l���Ƃ�g�����݂����A���͋ɏ��l�ɂȂ�Ȃ��ꍇ�B
�����͇@�A�A�������邯��LJA�̋ɏ��l�͍ŏ��l�ɂ͂Ȃ�Ȃ�
> �Ⴆ��-���܂ł�����ł��������l���Ƃ��ꍇ��A
>>948 x<1 �̂Ƃ��@1/t �� 1/tt,
�@��[x,1] (1/t) dt �� ��[x,1] (1/tt) dt,
x>1 �̂Ƃ��@1/t �� 1/tt,
�@��[1,x] (1/t) dt �� ��[1,x] (1/tt) dt,
>>920 �܂����̊��ɍŏ��l�����鎖�͖w�ǎ����ɂ킩�邩�炻���f���ċc�_����Ώؖ��Ƃ��Ă͐��藧��
>>959 ���肪�Ƃ��������܂��I
���������ŏ��l�����݂��邱�Ƃ��ؖ����Ȃ��ƃ_�����Ă��Ƃł��ˁc
������ȒP�Ɏ������@�������肵�܂���
>>964 �� xlogx �� x��0 �ɘA���Ɋg���ł��鎖���g���ΊȒP�B
��������Ɓ@GL(n,R)�̑S�Ă̌�����邱�ƂƓ��l������A
1�����x�N�g����Ԃ̏ꍇ���l����Ηǂ��ł���
���̊p�x�����Ă���
�]�g���A�v���̈��
���̖��͗e�Ղ�������̂ɂ��ꂾ����������Ȃ��A���������ꏏ�ɋ����Ă����Ə�����
�ǂ̌����g�����
>>969 ���������̎O�p�`�����ɐ܂�Ԃ��ĉ~���p�̒藝����x=50���B
50
>>969 �p�x���������A�Ƃ����������Ȃ��̂ŁA���a��̉����₷���_�Ōv�Z���ėǂ�
�������͉E���̐܂�Ԃ��Ă������S��������
��������߂Č����������������Ă�낤���ǂ��������Ȃ�����\���Ƃ�
>>969 �ǂ��炩�̎O�p�`��I��ŁA���a�őΏ̂ȎO�p�`��`�悷��
���Ƃ͉~���p
�~���p���I�I�I�I�Ȃ�قNjC��������
>>973 �̕��j�Ł�=90���Ƃ���ƁA
���E�̎O�p�`�̏�̒��_���d�Ȃ邩��A
���̎O�p�`�̏�̒��_��40���Ax=90��-40��=50��
������ĂȂ�Ő܂�Ԃ��Ɖ�����́H���̏������́H
�Ώ̐��ʼn~���p�̒藝���g����p�^�[���ɂȂ�
�O
>>969 �ς��ƌ�40�����炢�����Ȃ��ˁH
50~40�x���炢�Ȍ����ڂ���
�ӎO�p�`������āA�Ƃ��O�p���A�Ƃ��ōׁX�v�Z�����镪�̏�~���p�̒藝�ɓ����Ă���
>>979 ������Ă���킯�ł͂Ȃ��A�^����ꂽ��g����悤�ɂȂ���Ă��Ƃ���Ȃ�����
���̐}���Ɗp�x�������Ǝ�����Ă�������ǂ��g�������̂��킩���
�܂�Ԃ��ƒ������o���オ�邱�Ƃ��킩��
�O
>>981 �ς��ƌ�x=40��
�܂��͐}�ɃA���t�@�x�b�g�̕���������B�������ʒu�ɂ��钸�_��A�Ƃ��č�����BCD�ƒ��a�o�R�ŒႢ�ق��̒��_D���璼�a���E�ɖ߂�̂����R���ƁB
DE��AC�̌�_��F�Ƃ���B
��BCA=40��=��ECF
��OAB=50��
��BOA=80��
��AOC=100��
�K�v�Ȃ���������Ȃ�����E��ʂ���BC�ɐ����Ȓ����������B
��EAO=10���Ƃ���ƁA
��OEA=70���ƂȂ�A
��DEC=70��
��CAO=40��������A
��CAE=��CAO-��EAO=30��
x=40���Ȃ�A
��CDE+��DCA=��CFE
x+30��=70���ƂȂ��Ă��傤�ǂ����B
AE//DC�ƂȂ�Ƃ킩���Đ}���c��ł��Ƃ킩��B
������뒼������āA
x=40���Ŗ����Ȃ��B
�O
>>986 �����B
��BCD=65��
��EAO=15��
��CAE=25��
x=50���̂ق������R�������B
xyz+x+y+z-xy-yz-zx-1=(x-1)(y-1)(z-1)
���W���܂Ƃ߂Ă��������̍�Ƃł�
>>956 �ǂȂ������̖������˂������܂�
�Ώ̐�����ς��ƌ��ł킩��Ǝv����
>>956 >>991 �⑫
ℝ����ℝ^2�ւ̘A���S�P�˂͑��݂��܂����H
�y�A�m�Ȑ����Ȃ�������ˁH
�y�A�m�Ȑ���R��R�O2�̒P�˂ł͂Ȃ�
���̃X���b�h�͂P�O�O�O���܂����B
5�����˂�̉^�c�̓v���~�A������̊F���܂Ɏx�����Ă��܂��B
�^�c�ɂ����͂��肢�������܂��B
��������������������������������������
�s�v���~�A������̎�ȓ��T�t
�� 5�����˂��p�u���E�U����̍L������
�� 5�����˂�̉ߋ����O���擾
�� �������K���̊ɘa
��������������������������������������
����o�^�ɂ͌l���͈�ؕK�v����܂���B
��300�~���瓽���ł��w�����������܂��B
�� �v���~�A������o�^�͂����� ��
https://premium.5ch.net/ �� �Q�l���O�C���͂����� ��
https://login.5ch.net/login.php
�j���[�X �X�|�[�c �Ȃ�ł� ����
���̃X���ւ̌Œ胊���N�F http://5chb.net/r/math/1562421561/ �q���g�F http ://xxxx.5chb .net/xxxx �̂悤��b �����邾���ł����ŃX���ۑ��A�{���ł��܂��BTOP�� TOP�� �@
�S�f���ꗗ ���̌f���� �l�C�X�� |
Youtube ����
>50
>100
>200
>300
>500
>1000��
�V���摜 ���u������Ȃ����͂����ɏ����Ă�454 YouTube����>2�{ ->�摜>37�� �v �������l�����Ă��܂��F�E������Ȃ����͂����ɏ����Ă�456 ������Ȃ����͂����ɏ����Ă�456 ������Ȃ����͂����ɏ����Ă�436 ������Ȃ����͂����ɏ����Ă�462 ������Ȃ����͂����ɏ����Ă�460 ������Ȃ����͂����ɏ����Ă�465 ������Ȃ����͂����ɏ����Ă�434 ������Ȃ����͂����ɏ����Ă�419 ������Ȃ����͂����ɏ����Ă�433 ������Ȃ����͂����ɏ����Ă�417 ������Ȃ����͂����ɏ����Ă�445 ������Ȃ����͂����ɏ����Ă�455 ������Ȃ����͂����ɏ����Ă�427 ������Ȃ����͂����ɏ����Ă�440 ������Ȃ����͂����ɏ����Ă�441 ������Ȃ����͂����ɏ����Ă�449 ������Ȃ����͂����ɏ����Ă�430 ������Ȃ����͂����ɏ����Ă�424 ������Ȃ����͂����ɏ����Ă�442 ������Ȃ����͂����ɏ����Ă�478 ������Ȃ����͂����ɏ����Ă�439 ������Ȃ����͂����ɏ����Ă�428 ������Ȃ����͂����ɏ����Ă�447 ������Ȃ����͂����ɏ����Ă�421 [���f�]�ڋ֎~]©2ch.net ������Ȃ����͂����ɏ����Ă�431 [���f�]�ڋ֎~]©2ch.net ������Ȃ����͂����ɏ����Ă�423 ������Ȃ����͂����ɏ����Ă�429 ������Ȃ����͂����ɏ����Ă�459 ������Ȃ����͂����ɏ����Ă� 467 ������Ȃ����͂����ɏ����Ă� 466 �}���ł�����͂����ɏ����Ă� 1 ������Ȃ����͂����ɏ����Ă�357 ������Ȃ����͂����ɏ����Ă� 472 ������Ȃ����͂����ɏ����Ă� 471 �� �킩��Ȃ����͂����ɏ����Ă� �P�U�R �� �}���ł��Ȃ����͂����ɂ����Ă�3 ������˂����͂����֏��� ver3.14(67����)4062 ������˂����͂����֏��� ������˂����͂����֏��� ver.3.14(34����)1971 �����Ƌ������́H ���w ��b��萸�u�̉��K���͂�������������H��������Ȃ��ĕ�����Â炢 ���ꂩ��苳���� �������ė~���� �N�����̖������Ă��� �ËL���w�ʼn����Ȃ����͖��� ���K���͉����K�v������̂� ���ꂩ���̐ϕ��̖��������Ă��� ���̖��̓e�C���[�W�J�ʼn����� 2�̕������ɂ��� Part.2 ���ꂩ���̖��������Ă��������I�I �̖�������̂ŁA�����ĕ]�����ĉ����� ��w�̖��͂���ԕ��ȏȂ����� (11) ���̖��������ė~�����B ���C�̍������������mite �ϕ������̖��ɂ��Ă̎���X�� �|�G���͂����ɏ����Ă� 5 �|�G���͂����ɏ����Ă� 4 �m���̖���₵������݂�ȉ����Ă��� ���������̘_�����\�ɂ��Ĉӌ�����X�� �������w���̖��ł��B���ꂩ�����Ă������� ���̖����Ƃ��ĖႦ�Ȃ��ł��傤��(�K�E�X�̏����@) ���C��5�N�ԍl���Ă������Ȃ��m���̖���N�������Ă���
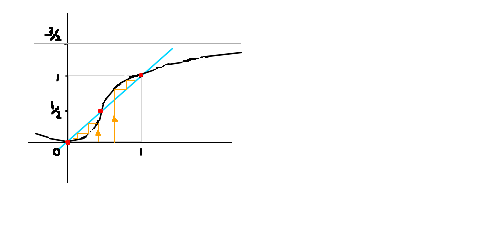

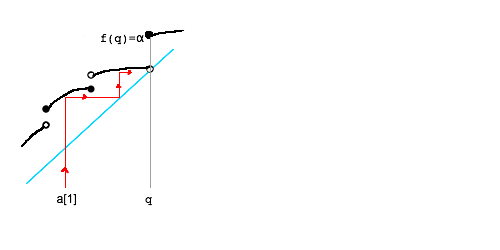

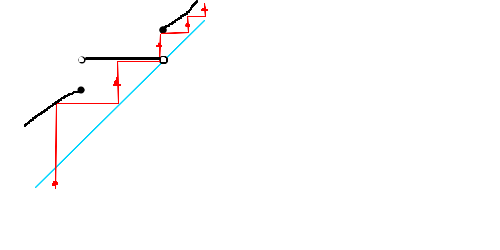
 )
)